题目内容
(本小题满分12分)
设函数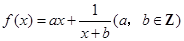 ,曲线
,曲线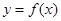 在点
在点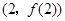 处的切线方程
处的切线方程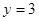 .
.
(1)求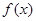 的解析式,并判断函数
的解析式,并判断函数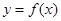 的图像是否为中心对称图形?若是,请求其对称中心;否则说明理由。
的图像是否为中心对称图形?若是,请求其对称中心;否则说明理由。
(2)证明:曲线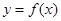 上任一点的切线与直线
上任一点的切线与直线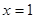 和直线
和直线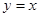 所围三角形的面积为定值,并求出此定值.
所围三角形的面积为定值,并求出此定值.
(3) 将函数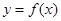 的图象向左平移一个单位后与抛物线
的图象向左平移一个单位后与抛物线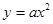 (
(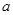 为非0常数)的图象有几个交点?(说明理由)
为非0常数)的图象有几个交点?(说明理由)
设函数
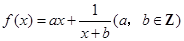 ,曲线
,曲线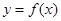 在点
在点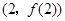 处的切线方程
处的切线方程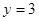 .
.(1)求
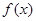 的解析式,并判断函数
的解析式,并判断函数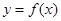 的图像是否为中心对称图形?若是,请求其对称中心;否则说明理由。
的图像是否为中心对称图形?若是,请求其对称中心;否则说明理由。(2)证明:曲线
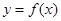 上任一点的切线与直线
上任一点的切线与直线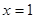 和直线
和直线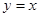 所围三角形的面积为定值,并求出此定值.
所围三角形的面积为定值,并求出此定值.(3) 将函数
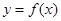 的图象向左平移一个单位后与抛物线
的图象向左平移一个单位后与抛物线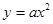 (
(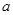 为非0常数)的图象有几个交点?(说明理由)
为非0常数)的图象有几个交点?(说明理由)(1) 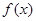 的图像是以点
的图像是以点 为中心的中心对称图形.
为中心的中心对称图形.
(2) 三角形的面积为定值
(3) 由三次函数的图象是连续的可知F(x)至少有一零点
当 时
时 在R上为减函数(减函数至多有一个零点),
在R上为减函数(减函数至多有一个零点),
所以此时F(x)有且只有一个零点;
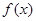 的图像是以点
的图像是以点 为中心的中心对称图形.
为中心的中心对称图形.(2) 三角形的面积为定值

(3) 由三次函数的图象是连续的可知F(x)至少有一零点

当
 时
时 在R上为减函数(减函数至多有一个零点),
在R上为减函数(减函数至多有一个零点), 所以此时F(x)有且只有一个零点;
试题分析:解:(1)
 ,
, 曲线
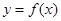 在点
在点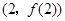 处的切线方程为y=3,
处的切线方程为y=3,于是
 解得
解得 或
或
因
 ,故
,故 .
.  ,满足
,满足 ,所以
,所以 是奇函数
是奇函数 所以,其图像是以原点(0,0)为中心的中心对称图形.
而函数
 的图像按向量
的图像按向量 平移,即得到函数
平移,即得到函数 的图像,
的图像,故函数
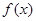 的图像是以点
的图像是以点 为中心的中心对称图形.
为中心的中心对称图形. (2)证明:在曲线上任取一点
 . 由
. 由 知,
知, 过此点的切线方程为
 .
. 令
 得
得 ,切线与直线
,切线与直线 交点为
交点为 .
. 令
 得
得 ,切线与直线
,切线与直线 交点为
交点为 .
.直线
 与直线
与直线 的交点为
的交点为 .
. 从而所围三角形的面积为
 .
. 所以,所围三角形的面积为定值
 .
. (3)将函数
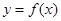 的图象向左平移一个单位后得到的函数为
的图象向左平移一个单位后得到的函数为 ,
,它与抛物线
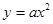 的交点个数等于方程
的交点个数等于方程 =
= 的解的个数
的解的个数 法一:
即
 (
( 解的个数,(易知0不是其解,不产生增根)
解的个数,(易知0不是其解,不产生增根) 即
 的零点(与x轴交点的横坐标)的个数
的零点(与x轴交点的横坐标)的个数 
由三次函数的图象是连续的可知F(x)至少有一零点 11分

当
 时
时 在R上为减函数(减函数至多有一个零点),
在R上为减函数(减函数至多有一个零点), 所以此时F(x)有且只有一个零点;
点评:解决的关键是能结合导数的几何意义表示切线方程,进而分析函数的零点个数,需要对于a分类讨论得到,属于中档题。

练习册系列答案
 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
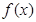 和
和 的图象关于原点对称,且
的图象关于原点对称,且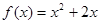 .
. 在[-1,1]上是增函数,求实数
在[-1,1]上是增函数,求实数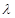 的取值范围
的取值范围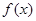 是定义在
是定义在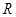 上的函数,且
上的函数,且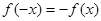 ,当
,当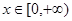 时,
时,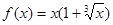 ,那么当
,那么当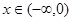 时,
时,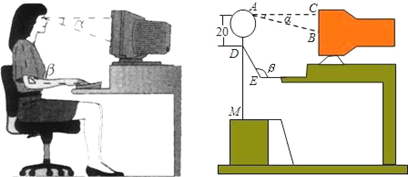
 上的偶函数
上的偶函数 满足
满足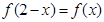 ,且在
,且在 上是减函数,
上是减函数, 是钝角三角形的两个锐角,则下列结论正确的是( )
是钝角三角形的两个锐角,则下列结论正确的是( )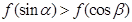
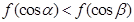

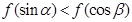
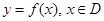 ,若存在常数C,对任意的
,若存在常数C,对任意的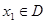 ,存在唯一的
,存在唯一的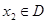 ,使得
,使得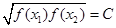 ,则称函数
,则称函数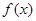 在D上的几何平均数为C.已知
在D上的几何平均数为C.已知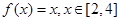 ,则函数
,则函数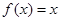 在
在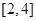 上的几何平均数为( )
上的几何平均数为( ) 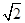 B.
B.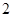 C.
C.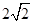 D.
D.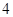
 的连续函数
的连续函数 ,对任意
,对任意 都有
都有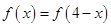 ,且其导函数
,且其导函数 满足
满足 ,则当
,则当 时,有( )
时,有( )

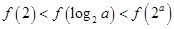

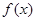 的图象是折线段
的图象是折线段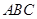 ,其中
,其中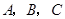 的坐标分别为
的坐标分别为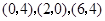 ,则
,则 。
。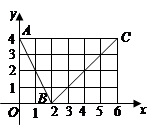
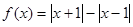 是奇函数;②
是奇函数;② 既不是奇函数也不是偶函数;③
既不是奇函数也不是偶函数;③
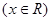 是偶函数 ;④
是偶函数 ;④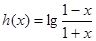 是奇函数.其中正确的有( )个
是奇函数.其中正确的有( )个