题目内容
1.已知a是实数,函数f(x)=$\sqrt{x}$(x-a).求函数f(x)的单调区间.分析 求函数的导数,利用函数单调性和导数之间的关系进行判断即可.
解答 解:函数的定义域为[0,+∞),
f(x)=$\sqrt{x}$(x-a)=x${\;}^{\frac{3}{2}}$-a•x${\;}^{\frac{1}{2}}$.
函数的导数f′(x)=$\frac{3}{2}$x${\;}^{\frac{1}{2}}$-$\frac{a}{2\sqrt{x}}$=)=$\frac{3}{2}$$\sqrt{x}$-$\frac{a}{2\sqrt{x}}$=$\frac{3x-a}{2\sqrt{x}}$,
若a≤0,则f′(x)≥0恒成立,此时函数单调递增,即函数的单调递增区间为[0,+∞),
若a>0,
由f′(x)>0得x>$\frac{a}{3}$,此时函数单调递增,即函数的单调递增区间为[$\frac{a}{3}$,+∞).
由f′(x)<0得0≤x<$\frac{a}{3}$,此时函数单调递减,即函数的单调递减区间为[0,$\frac{a}{3}$).
点评 本题主要考查函数的单调区间的求解,求函数的导数,利用函数单调性和导数之间的关系是解决本题的关键.注意要对a进行分类讨论.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
10.在△ABC中,∠A,∠B,∠C所对应的边分别为a,b,c,若2∠B=∠A+∠C,且a=1,b=$\sqrt{3}$,则S△ABC=( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | 2 |
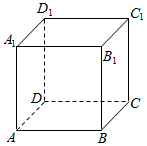 在正方体ABCD-A1B1C1D1中,求下列异面直线所成角的大小
在正方体ABCD-A1B1C1D1中,求下列异面直线所成角的大小 在多面体ABCDEF中,底面ABCD是梯形,四边形ADEF是正方形.AB∥DC,AB=AD=1,CD=2,AC=EC=$\sqrt{5}$.
在多面体ABCDEF中,底面ABCD是梯形,四边形ADEF是正方形.AB∥DC,AB=AD=1,CD=2,AC=EC=$\sqrt{5}$.