题目内容
2.(x2-$\frac{1}{2x}$)6的展开式中,常数项是( )| A. | $\frac{15}{16}$ | B. | $\frac{5}{4}$ | C. | -$\frac{15}{16}$ | D. | -$\frac{5}{4}$ |
分析 Tr+1=$(-\frac{1}{2})^{r}$${∁}_{6}^{r}$x12-3r,令12-3r=0,解得r即可得出.
解答 解:Tr+1=${∁}_{6}^{r}$(x2)6-r$(-\frac{1}{2x})^{r}$=$(-\frac{1}{2})^{r}$${∁}_{6}^{r}$x12-3r,
令12-3r=0,解得r=4.
∴此常数项为:$(-\frac{1}{2})^{4}{∁}_{6}^{4}$=$\frac{15}{16}$.
故选:A.
点评 本题考查了二项式定理的应用,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
14.△ABC的三个内角A,B,C所对的边分别是a,b,c,若$a=2,c=\sqrt{19}$,$tanA+tanB=\sqrt{3}-\sqrt{3}tanAtanB$,则△ABC的面积S△ABC=( )
| A. | $\frac{{3\sqrt{3}}}{2}$ | B. | $\frac{3}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{1}{2}$ |
11.已知菱形ABCD的边长为4,$∠ABC=\frac{π}{6}$,若在菱形内取一点,则该点到菱形的四个顶点的距离均大于1的概率为( )
| A. | $\frac{π}{4}$ | B. | $1-\frac{π}{4}$ | C. | $\frac{π}{8}$ | D. | $1-\frac{π}{8}$ |
12.非负实数x、y满足ln(x+y-1)≤0,则关于x-y的最大值和最小值分别为( )
| A. | 2和1 | B. | 2和-1 | C. | 1和-1 | D. | 2和-2 |
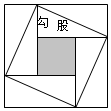 我国汉代数学家赵爽为了证明勾股定理,创制了一副“弦图”,后人称其为“赵爽弦图”.如图是该弦图变化得到,它是用八个全等的直角三角形拼接而成.若图中勾、股分别为2,5,一粒豆子随机投入大正方形中,则落到阴影部分(含边界)概率是$\frac{9}{49}$.
我国汉代数学家赵爽为了证明勾股定理,创制了一副“弦图”,后人称其为“赵爽弦图”.如图是该弦图变化得到,它是用八个全等的直角三角形拼接而成.若图中勾、股分别为2,5,一粒豆子随机投入大正方形中,则落到阴影部分(含边界)概率是$\frac{9}{49}$.