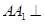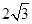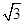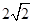题目内容
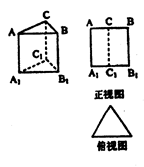
如图,四棱锥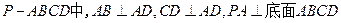 ,
,
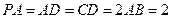 ,
,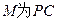 的中点.
的中点.
(1)求证: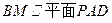 ;
;
(2)在侧面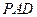 内找一点
内找一点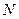 ,使
,使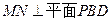 ,并求直线
,并求直线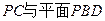 所成角的正弦值.
所成角的正弦值.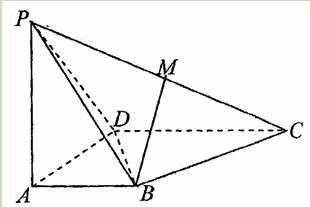
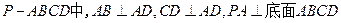 ,
,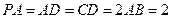 ,
,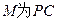 的中点.
的中点.(1)求证:
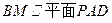 ;
;(2)在侧面
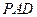 内找一点
内找一点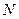 ,使
,使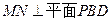 ,并求直线
,并求直线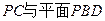 所成角的正弦值.
所成角的正弦值.
解(1)取 的中点
的中点 ,连接
,连接 则
则 ,且
,且
所以四边形 为平行四边形,所以
为平行四边形,所以 …………………………………………2分
…………………………………………2分
又 平面
平面 ,
, 不在平面
不在平面 内,
内, 平面
平面 ;………………………4分
;………………………4分
(2)以 为原点,
为原点, 分别为
分别为 轴,建立空间直角坐标系
轴,建立空间直角坐标系
则
假设存在满足题意的点,则在平面 内,设
内,设

 ,得
,得
所以 ,即
,即 是
是 的中点,此时
的中点,此时 平面
平面 ,…………………………8分
,…………………………8分
设直线 与平面
与平面 所成的角为
所成的角为 ,
,
易得
设 与
与 的夹角为
的夹角为 ,则
,则 …………………………………10分
…………………………………10分

故直线 与平面
与平面 所成角的正弦值为
所成角的正弦值为 ……………………………………………12分
……………………………………………12分
 的中点
的中点 ,连接
,连接 则
则 ,且
,且
所以四边形
 为平行四边形,所以
为平行四边形,所以 …………………………………………2分
…………………………………………2分又
 平面
平面 ,
, 不在平面
不在平面 内,
内, 平面
平面 ;………………………4分
;………………………4分(2)以
 为原点,
为原点, 分别为
分别为 轴,建立空间直角坐标系
轴,建立空间直角坐标系则

假设存在满足题意的点,则在平面
 内,设
内,设

 ,得
,得
所以
 ,即
,即 是
是 的中点,此时
的中点,此时 平面
平面 ,…………………………8分
,…………………………8分设直线
 与平面
与平面 所成的角为
所成的角为 ,
,易得

设
 与
与 的夹角为
的夹角为 ,则
,则 …………………………………10分
…………………………………10分
故直线
 与平面
与平面 所成角的正弦值为
所成角的正弦值为 ……………………………………………12分
……………………………………………12分略

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案
相关题目
 是线段EF的中点.
是线段EF的中点. ;(2)设二面角A—FD—B的大小为
;(2)设二面角A—FD—B的大小为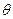 ,求
,求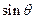 的值;
的值; 的路线运动到点C,求这一过程中形成的三棱锥P—BFD的体积的最小值.
的路线运动到点C,求这一过程中形成的三棱锥P—BFD的体积的最小值.




 的等边
的等边 的底边
的底边 与
与 轴平行,则用斜二测画法画出它的直观图的面积是( )
轴平行,则用斜二测画法画出它的直观图的面积是( )




 面ABCD,E为AB中点,求二面角E-SC-D的大小;
面ABCD,E为AB中点,求二面角E-SC-D的大小; EC的距离。
EC的距离。