题目内容
已知椭圆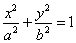
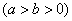 上的点到其两焦点距离之和为
上的点到其两焦点距离之和为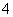 ,且过点
,且过点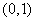 .
.
(Ⅰ)求椭圆方程;
(Ⅱ) 为坐标原点,斜率为
为坐标原点,斜率为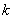 的直线过椭圆的右焦点,且与椭圆交于点
的直线过椭圆的右焦点,且与椭圆交于点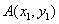 ,
,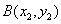 ,若
,若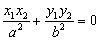 ,求△
,求△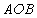 的面积.
的面积.
解(Ⅰ)依题意有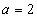 ,
, 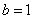 .
.
故椭圆方程为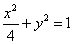 .
.
(Ⅱ)因为直线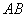 过右焦点
过右焦点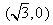 ,设直线
,设直线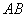 的方程为
的方程为 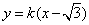 .
.
联立方程组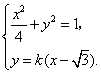
消去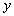 并整理得
并整理得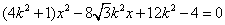 . (*)
. (*)
故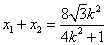 ,
,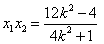 .
.
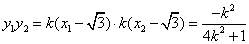 .
.
又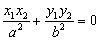 ,即
,即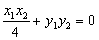 .
.
所以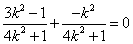 ,可得
,可得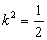 ,即
,即 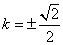 .
.
方程(*)可化为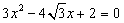 ,
,
由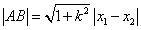 ,可得
,可得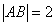 .
.
原点 到直线
到直线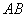 的距离
的距离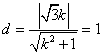 .
.
所以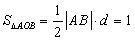 .
.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 分别是椭圆
分别是椭圆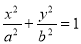
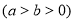 的上顶点和右焦点,直线
的上顶点和右焦点,直线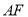 与椭圆交于另一点
与椭圆交于另一点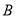 ,过中心
,过中心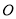 作直线
作直线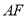 的平行线交椭圆于
的平行线交椭圆于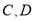 两点,若
两点,若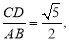 则椭圆的离心率为 .
则椭圆的离心率为 .
 的解集是 .
的解集是 .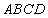 中,
中,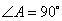 ,
,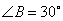 ,
,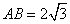 ,
,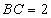 ,点
,点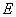 在线段
在线段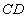 上,若
上,若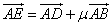 ,则
,则 的取值范围是
的取值范围是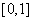 (B)
(B)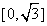 (C)
(C)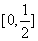 (D)
(D)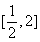
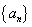 满足:公差
满足:公差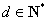 ,
,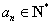 ,且
,且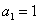 ,则
,则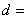 ; 若
; 若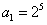 ,则
,则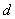 的所有可能取值之和为 .
的所有可能取值之和为 .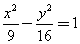 的右焦点,且平行其渐近线的直线方程是
的右焦点,且平行其渐近线的直线方程是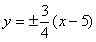 (B)
(B) 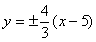
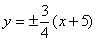 (D)
(D) 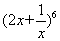 展开式中的常数项为 _________.
展开式中的常数项为 _________.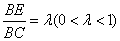 ,则满足
,则满足
 :
: (
( 为参数)的圆心坐标为__________;直线
为参数)的圆心坐标为__________;直线 :
: 被圆
被圆