题目内容
设数列{an}满足lgan+1=1+lgan,且a1+a2+…+a5=4,则a16+a17+…+a20=
- A.4•1015
- B.5•1015
- C.5•104
- D.4•104
A
分析:由对数函数的运算法则化简lgan+1=1+lgan,得到此数列为等比数列且得到公比q的值,然后把所求的式子提取q15后,把a1+a2+…+a5=4和求出的q代入即可求出值.
解答:由lgan+1=1+lgan=lg10+lgan=lg10an,
得到an+1=10an,
所以此数列是公比q=10的等比数列,
则a16+a17+…+a20=q15(a1+a2+…+a5)=4•1015.
故选A.
点评:此题考查学生灵活运用对数的运算法则化简求值,灵活运用等比数列的性质化简求值,是一道综合题.
分析:由对数函数的运算法则化简lgan+1=1+lgan,得到此数列为等比数列且得到公比q的值,然后把所求的式子提取q15后,把a1+a2+…+a5=4和求出的q代入即可求出值.
解答:由lgan+1=1+lgan=lg10+lgan=lg10an,
得到an+1=10an,
所以此数列是公比q=10的等比数列,
则a16+a17+…+a20=q15(a1+a2+…+a5)=4•1015.
故选A.
点评:此题考查学生灵活运用对数的运算法则化简求值,灵活运用等比数列的性质化简求值,是一道综合题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 满足f(2)=1,且方程f(x)=x有且仅有一个实数根.
满足f(2)=1,且方程f(x)=x有且仅有一个实数根. ,对于(Ⅱ)中的数列{an},令
,对于(Ⅱ)中的数列{an},令 ,设Sn为数列{bn}的前n项和,求证:Sn>ln(n+1).
,设Sn为数列{bn}的前n项和,求证:Sn>ln(n+1). 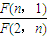 ,若Sn为数列{
,若Sn为数列{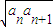 }的前n项和,则下列说法正确的是( )
}的前n项和,则下列说法正确的是( )