题目内容
12．掷一枚均匀的硬币4次，出现正面向上的次数不少于反面向上的次数的概率为（ ）| A． | $\frac{5}{16}$ | B． | $\frac{1}{2}$ | C． | $\frac{5}{8}$ | D． | $\frac{11}{16}$ |
分析 先求出基本事件总数n=24=16，再求出出现正面向上的次数不少于反面向上的次数包含的基本事件个数，由此能求出出现正面向上的次数不少于反面向上的概率．
解答 解：掷一枚均匀的硬币4次，基本事件总数n=24=16，
出现正面向上的次数不少于反面向上的次数包含的基本事件个数为：
m=${C}_{4}^{2}+{C}_{4}^{3}+{C}_{4}^{4}$=11，
∴出现正面向上的次数不少于反面向上的概率P=$\frac{11}{16}$．
故选：D．
点评 本题考查概率的求法，是基础题，解题时要认真审题，注意等可能事件概率计算公式的合理运用．
练习册系列答案
相关题目
20．
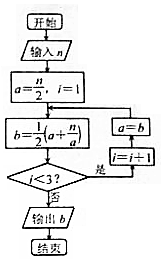一种在实数域和复数域上近似求解方程的方法可以设计如图所示的程序框图，若输入的n=12，则输出的结果b=（ ）
一种在实数域和复数域上近似求解方程的方法可以设计如图所示的程序框图，若输入的n=12，则输出的结果b=（ ）| A． | 4 | B． | $\frac{7}{2}$ | C． | $\frac{97}{28}$ | D． | $\frac{64}{14}$ |
17．已知函数f（x）=$\frac{1+lnx}{x}$，若关于x的不等式f2（x）+af（x）＞0恰有两个整数解，则实数a的取值范围是（ ）
| A． | （-$\frac{1+ln2}{2}$，-$\frac{1+ln3}{3}$） | B． | [$\frac{1+ln3}{3}$，$\frac{1+ln2}{2}$） | C． | （-$\frac{1+ln2}{2}$，-$\frac{1+ln3}{3}$] | D． | （-1，-$\frac{1+ln3}{3}$] |
1．双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（{a＞0，b＞0}）$的左、右焦点分别为F1，F2，过F1作x轴的垂线交双曲线于A，B两点，若$∠A{F_2}B＜\frac{π}{3}$，则双曲线离心率的取值范围是（ ）
| A． | $（{1，\sqrt{3}}）$ | B． | $（{1，\sqrt{6}}）$ | C． | $（{1，2\sqrt{3}}）$ | D． | $（{\sqrt{3}，3\sqrt{3}}）$ |
2．《张丘建算经》中女子织布问题为：某女子善于织布，一天比一天织得快，且从第2天开始，每天比前一天多织相同量的布，已知第一天织5尺布，一月（按30天计）共织390尺布，则从第2天起每天比前一天多织（ ）尺布．
| A． | $\frac{16}{31}$ | B． | $\frac{16}{29}$ | C． | $\frac{1}{2}$ | D． | $\frac{8}{15}$ |