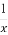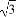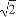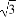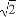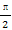题目内容
已知a,b,c为△ABC的三个内角A,B,C的对边,向量m=(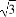 ,-1),n=(cosA,sinA).若m⊥n,且acosB+bcosA=csinC,则角A,B的大小分别为( )
,-1),n=(cosA,sinA).若m⊥n,且acosB+bcosA=csinC,则角A,B的大小分别为( )
(A)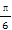 ,
,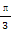 (B)
(B)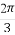 ,
,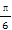
(C)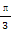 ,
,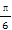 (D)
(D)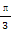 ,
,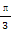
C
【解析】由m⊥n可得m·n=0,
即 cosA-sinA=0,所以A=
cosA-sinA=0,所以A= .
.
又acosB+bcosA=csinC知c=csinC,则sinC=1,所以C= ,由B=
,由B= -C可得B=
-C可得B= .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目