题目内容
设数列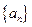 的前
的前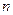 项和为
项和为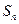 ,点
,点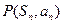 在直线
在直线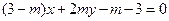 上,
上,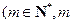 为常数,
为常数,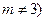 .
.
(Ⅰ)求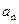 ;
;
(Ⅱ)若数列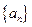 的公比
的公比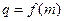 ,数列
,数列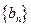 满足
满足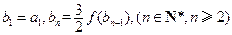 ,求证:
,求证: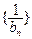 为等差数列,并求
为等差数列,并求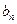 ;
;
(III)设数列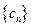 满足
满足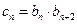 ,
,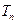 为数列
为数列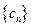 的前
的前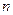 项和,且存在实数
项和,且存在实数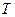 满足
满足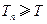 ,
,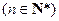 ,求
,求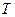 的最大值.
的最大值.
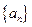 的前
的前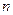 项和为
项和为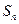 ,点
,点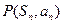 在直线
在直线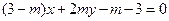 上,
上,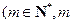 为常数,
为常数,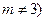 .
.(Ⅰ)求
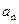 ;
;(Ⅱ)若数列
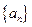 的公比
的公比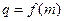 ,数列
,数列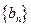 满足
满足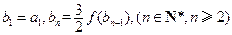 ,求证:
,求证: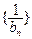 为等差数列,并求
为等差数列,并求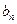 ;
;(III)设数列
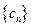 满足
满足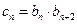 ,
,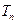 为数列
为数列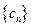 的前
的前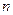 项和,且存在实数
项和,且存在实数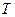 满足
满足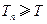 ,
,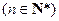 ,求
,求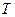 的最大值.
的最大值.(1)
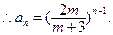
(2)略
(3)
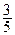
解:(Ⅰ)由题设,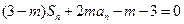 ①………………1分
①………………1分
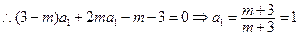
由①,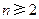 时,
时,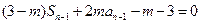
①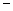 ②得,
②得,
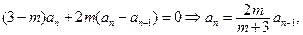
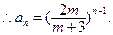 …………………………………………………………4分
…………………………………………………………4分
(Ⅱ)由(Ⅰ)知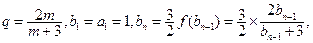
化简得: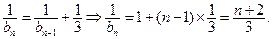 …………………………6分
…………………………6分
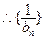 为等差数列,
为等差数列,
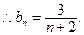 …………………………………………………………………8分
…………………………………………………………………8分
(III)由(Ⅱ)知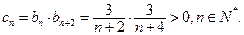 [
[
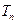 为数列
为数列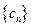 的前
的前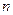 项和,因为
项和,因为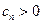 ,
,
所以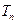 是递增的,
是递增的, 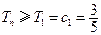 .………………………………………10分
.………………………………………10分
所以要满足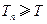 ,
,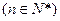 ,
,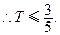
所以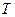 的最大值是
的最大值是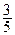 .……………………………………
.……………………………………
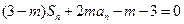 ①………………1分
①………………1分 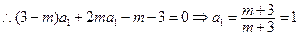
由①,
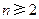 时,
时,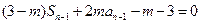
①
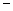 ②得,
②得,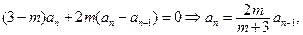
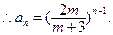 …………………………………………………………4分
…………………………………………………………4分 (Ⅱ)由(Ⅰ)知
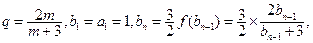
化简得:
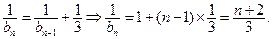 …………………………6分
…………………………6分 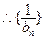 为等差数列,
为等差数列,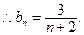 …………………………………………………………………8分
…………………………………………………………………8分 (III)由(Ⅱ)知
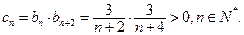 [
[ 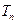 为数列
为数列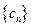 的前
的前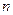 项和,因为
项和,因为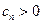 ,
,所以
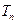 是递增的,
是递增的, 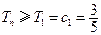 .………………………………………10分
.………………………………………10分 所以要满足
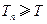 ,
,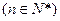 ,
,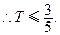
所以
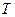 的最大值是
的最大值是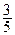 .……………………………………
.……………………………………
练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
相关题目
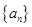 为等差数列,
为等差数列,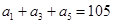 ,
,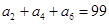 ,
, 是等差数列
是等差数列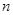 项和,则使得
项和,则使得 对
对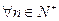 都有
都有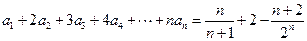
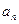 ;
; 的前n项和为
的前n项和为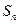 , 求证:对
, 求证:对 .
.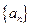 中,
中,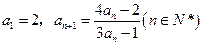 ,设
,设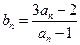 .
.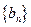 的前三项;
的前三项;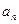 ;
;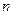 项和为
项和为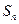 ,求证:
,求证: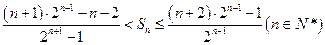 .
.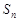 为等差数列
为等差数列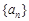 的前
的前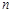 项和,且
项和,且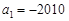 ,
,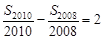 ,则
,则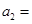 ( )
( )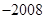
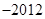
 N*),满足条件:
N*),满足条件: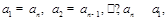 即
即 ,我们称其为“对称数列”.例如:数列1,2,3,4,3,2,1就是“对称数列”.已知数列
,我们称其为“对称数列”.例如:数列1,2,3,4,3,2,1就是“对称数列”.已知数列 是项数为不超过
是项数为不超过 的“对称数列”,并使得1,2,22,…,
的“对称数列”,并使得1,2,22,…, 依次为该数列中前连续的
依次为该数列中前连续的 项,则数列
项,则数列 可以是:
可以是: ①
① ;②
;② ; ③
; ③ ;④
;④ .
.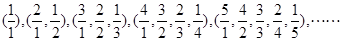
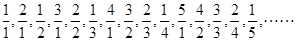
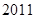 项是( )
项是( )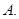
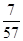
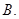
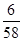
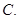
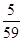
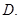
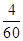
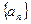 中,
中,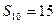 则
则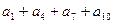 =( )
=( )