题目内容
(本题满分13分)
已知数列 对
对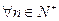 都有
都有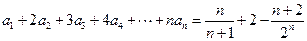
(Ⅰ) 求 的通项
的通项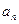 ;
;
(Ⅱ) 设数列
 的前n项和为
的前n项和为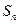 , 求证:对
, 求证:对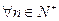 ,
,  .
.
已知数列
 对
对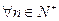 都有
都有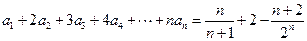
(Ⅰ) 求
 的通项
的通项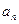 ;
;(Ⅱ) 设数列

 的前n项和为
的前n项和为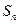 , 求证:对
, 求证:对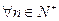 ,
,  .
.(Ⅰ)

(Ⅱ) 证明略
(Ⅰ) 解:

 显然对n=1也成立
显然对n=1也成立  -------------6分
-------------6分
(Ⅱ) 证明:显然 递增,
递增, ------------8分
------------8分

 -----------13分
-----------13分

 显然对n=1也成立
显然对n=1也成立  -------------6分
-------------6分(Ⅱ) 证明:显然
 递增,
递增, ------------8分
------------8分
 -----------13分
-----------13分
练习册系列答案
相关题目
 中,
中, ,则数列
,则数列 ( )
( )





 的前
的前 项和为
项和为 ,点
,点 均在
均在 函数
函数 的图象上
的图象上 的通项公式
的通项公式 的首项是1,公比为
的首项是1,公比为 的等比数列,求数列
的等比数列,求数列 的前
的前
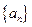 的前
的前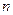 项和为
项和为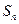 ,点
,点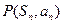 在直线
在直线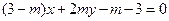 上,
上,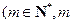 为常数,
为常数,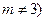 .
.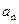 ;
;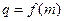 ,数列
,数列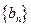 满足
满足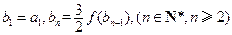 ,求证:
,求证: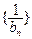 为等差数列,并求
为等差数列,并求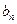 ;
;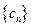 满足
满足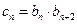 ,
,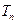 为数列
为数列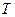 满足
满足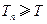 ,
,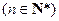 ,求
,求 中,
中, ,
,
 满足
满足 =
= ,求数列
,求数列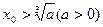 ,由递推公式
,由递推公式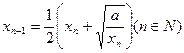 得到数列
得到数列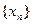 ,对于任意的
,对于任意的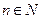 ,都有
,都有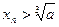 ,用数列
,用数列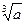 的近似值。
的近似值。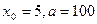 ,计算
,计算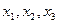 的值(精确到0.01);归纳出
的值(精确到0.01);归纳出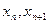 的大小关系;
的大小关系;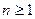 时,证明:
时,证明: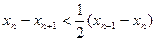 ;
;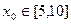 时,用数列
时,用数列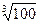 的近似值,要求
的近似值,要求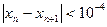 ,请你估计n,并说明理由
,请你估计n,并说明理由 ,
, ,4成等差数列,1,
,4成等差数列,1, ,
, ,
, ,4成等比数列,则
,4成等比数列,则 .
.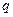 ,每列上的数从上到下都成等差数列,正数
,每列上的数从上到下都成等差数列,正数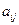 表示位于第
表示位于第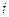 行第
行第 列的数,其中
列的数,其中
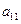
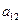

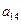







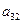
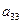

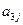



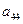


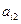


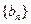 满足
满足 的前
的前 项和为
项和为 ,
, 的大小,并说明理由。
的大小,并说明理由。