题目内容
6.下列结论中错误的是( )| A. | 若0<α<$\frac{π}{2}$,则sin α<tan α | |
| B. | 若α是第二象限角,则$\frac{α}{2}$为第一象限角或第三象限角 | |
| C. | 若角α的终边过点P(3k,4k)且k≠0,则sin α=$\frac{4}{5}$ | |
| D. | 若α=-$\frac{π}{3}$,则cos α=$\frac{1}{2}$ |
分析 利用任意角的三角函数的定义,象限角的定义,判断各个选项是否正确,从而得出结论.
解答 解:若0<α<$\frac{π}{2}$,则sinα<tanα=$\frac{sinα}{cosα}$,故A正确;
若α是第二象限角,即α(2kπ,2kπ+π),k∈Z,则$\frac{α}{2}$∈(kπ,kπ+$\frac{π}{2}$),为第一象限或第三象限,故B正确;
若角α的终边过点P(3k,4k)(k≠0),则sinα=$\frac{4k}{\sqrt{9{k}^{2}+16{k}^{2}}}$=$\frac{4k}{5|k|}$,不一定等于$\frac{4}{5}$,故C不正确;
若α=-$\frac{π}{3}$,则cos α=$\frac{1}{2}$,故D正确
故选:C.
点评 本题主要考查任意角的三角函数的定义,象限角的判定,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.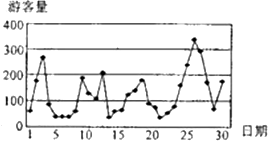 已知云台山景区对拥挤等级与每日游客数量(单位:百人)的关系有如下规定:当n∈[0,100)时,拥挤等级为“优”;当n∈[100,200)时,拥挤等级为“良”;当n∈[200,300)时,拥挤等级为“拥挤”;当n≥300时,拥挤等级为“严重拥挤”.该景区对9月份的游客数量作出如图的统计数据.
已知云台山景区对拥挤等级与每日游客数量(单位:百人)的关系有如下规定:当n∈[0,100)时,拥挤等级为“优”;当n∈[100,200)时,拥挤等级为“良”;当n∈[200,300)时,拥挤等级为“拥挤”;当n≥300时,拥挤等级为“严重拥挤”.该景区对9月份的游客数量作出如图的统计数据.
(1)下面是根据统计数据得到的频率分布直方表,求出a,b,c的值,并估计该景区9月份游客人数的平均值(同一组中的数据用该组区间的中点值作代表);
(2)某人选择在9月1日至9月5日这5天中任选2天到该景区游玩,求他这2天遇到的游客拥挤等级均为“优”的概率.
 已知云台山景区对拥挤等级与每日游客数量(单位:百人)的关系有如下规定:当n∈[0,100)时,拥挤等级为“优”;当n∈[100,200)时,拥挤等级为“良”;当n∈[200,300)时,拥挤等级为“拥挤”;当n≥300时,拥挤等级为“严重拥挤”.该景区对9月份的游客数量作出如图的统计数据.
已知云台山景区对拥挤等级与每日游客数量(单位:百人)的关系有如下规定:当n∈[0,100)时,拥挤等级为“优”;当n∈[100,200)时,拥挤等级为“良”;当n∈[200,300)时,拥挤等级为“拥挤”;当n≥300时,拥挤等级为“严重拥挤”.该景区对9月份的游客数量作出如图的统计数据.(1)下面是根据统计数据得到的频率分布直方表,求出a,b,c的值,并估计该景区9月份游客人数的平均值(同一组中的数据用该组区间的中点值作代表);
| 游客数量 (单位:百人) | [0,100) | [100,200) | [200,300) | [300,400) |
| 天数 | a | 10 | 4 | c |
| 频率 | b | $\frac{1}{3}$ | $\frac{2}{15}$ | $\frac{1}{30}$ |
11.已知向量$\overrightarrow{a}$=(an,2),$\overrightarrow{b}$=(an+1,$\frac{2}{5}$),且a1=1,若数列{an}的前n项和为Sn,且$\overrightarrow{a}$∥$\overrightarrow{b}$,则Sn=( )
| A. | $\frac{5}{4}$[1-($\frac{1}{5}$)n] | B. | $\frac{1}{4}$[1-($\frac{1}{5}$)n] | C. | $\frac{1}{4}$[1-($\frac{1}{5}$)n-1] | D. | $\frac{5}{4}$[1-($\frac{1}{5}$)n-1] |
15.已知复数z满足($\sqrt{3}$+3i)z=3i,则|z|=( )
| A. | $\sqrt{2}$ | B. | 1 | C. | $\sqrt{3}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
16.?x∈[-2,1],使不等式ax3-x2+4x+3≥0成立,则实数a的取值范围是( )
| A. | [-5,-3] | B. | [-6,-$\frac{9}{8}$] | C. | [-6,-2] | D. | [-4,-3] |
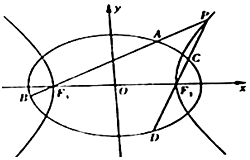 如图,已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\;\;(a>b>0)$的离心率为$\frac{{\sqrt{2}}}{2}$,以该椭圆上的点和椭圆的左、右焦点F1,F2为顶点的三角形的周长为$4(\sqrt{2}+1)$,一等轴双曲线的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的交点分别为A、B和C、D.
如图,已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\;\;(a>b>0)$的离心率为$\frac{{\sqrt{2}}}{2}$,以该椭圆上的点和椭圆的左、右焦点F1,F2为顶点的三角形的周长为$4(\sqrt{2}+1)$,一等轴双曲线的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的交点分别为A、B和C、D.