题目内容
 从甲、乙两名学生的若干次数学成绩中随机抽取6次,制得成绩数据的茎叶图如图所示.
从甲、乙两名学生的若干次数学成绩中随机抽取6次,制得成绩数据的茎叶图如图所示.(Ⅰ)根据茎叶图,求甲、乙两名学生的数学成绩的方差;
(Ⅱ)现从乙学生这6次数学成绩中随机抽取2次成绩,求这2次成绩至少有一次不低于85分的概率.
分析:(I)根据茎叶图,我们结合甲乙两名学生的成绩,我们可以求出两个人的平均成绩,进而计算出两个人的方差(或标准差);
(II)乙学生这6次数学成绩中,不低于85分的有3次,计算随机抽取2次成绩的所有情况种数;求出其中2次成绩至少有一次不低于85分的情况种数,利用古典概型概率公式计算.
(II)乙学生这6次数学成绩中,不低于85分的有3次,计算随机抽取2次成绩的所有情况种数;求出其中2次成绩至少有一次不低于85分的情况种数,利用古典概型概率公式计算.
解答:解:(1)由样本数据得
=
=85,
=
=85,可知甲、乙学生平均水平相同;
由样本数据得s甲2=
[(85-77)2+(85-78)2+(85-81)2+(85-86)2+(85-93)2+(85-95)2]=49,
s乙2=
[(85-76)2+(85-80)2+(85-82)2+(85-85)2+(85-92)2+(85-95)2]=44,
乙学生比甲学生发挥更稳定.
(2)乙学生这6次数学成绩中,不低于85分的有3次,
随机抽取2次成绩有
=15种情况.
其中2次成绩至少有一次不低于85分的有
+
×
=12种情况,
∴这2次成绩至少有一次不低于85分的概率为
=
.
. |
| x甲 |
| 77+78+81+86+93+95 |
| 6 |
. |
| x乙 |
| 76+80+82+85+92+95 |
| 6 |
由样本数据得s甲2=
| 1 |
| 6 |
s乙2=
| 1 |
| 6 |
乙学生比甲学生发挥更稳定.
(2)乙学生这6次数学成绩中,不低于85分的有3次,
随机抽取2次成绩有
| C | 2 6 |
其中2次成绩至少有一次不低于85分的有
| C | 2 3 |
| C | 1 3 |
| C | 1 3 |
∴这2次成绩至少有一次不低于85分的概率为
| 12 |
| 15 |
| 4 |
| 5 |
点评:本题考查古典概型及其概率计算公式,茎叶图,是统计和概率知识的综合考查,熟练掌握古典概型求解概率的方法和步骤是解答本题的关键.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
 某学校为了了解高三学生月考的数学成绩,从甲、乙两班各抽取10名学生,并统计他们的成绩(成绩均为整数且满分为100分),成绩如下:
某学校为了了解高三学生月考的数学成绩,从甲、乙两班各抽取10名学生,并统计他们的成绩(成绩均为整数且满分为100分),成绩如下: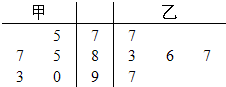 (2012•江门一模)甲、乙两名同学在5次英语口语测试中的成绩统计如图的茎叶图所示.
(2012•江门一模)甲、乙两名同学在5次英语口语测试中的成绩统计如图的茎叶图所示. 甲、乙两名同学在5次英语口语测试中的成绩统计如图所示.
甲、乙两名同学在5次英语口语测试中的成绩统计如图所示.