题目内容
7.已知函数f(x)=(sinx+cos)2+2$\sqrt{3}$sin2x(1)求函数f(x)的最小正周期并求出单调递增区间;
(2)在△ABC中,角A,B,C的对边分别是a,b,c,且满足2acosC+c=2b,求f(B)的取值范围.
分析 (1)利用三角函数的恒等变换化简函数的解析式为f(x)=2sin(2x-$\frac{π}{3}$)+1+$\sqrt{3}$,由此求得函数f(x)的最小正周期.
(2)在△ABC中,由条件利用余弦定理求得cosA的值,可得A的值,可得B的范围,再利用正弦函数的定义域和值域求得f(B)的范围.
解答 解:(1)函数f(x)=(sinx+cos)2+2$\sqrt{3}$sin2x=1+sin2x+2$\sqrt{3}$•$\frac{1-cos2x}{2}$
=sin2x-$\sqrt{3}$cos2x+1+$\sqrt{3}$=2sin(2x-$\frac{π}{3}$)+1+$\sqrt{3}$的最小正周期为$\frac{2π}{2}$=π.
令2kπ-$\frac{π}{2}$≤2x-$\frac{π}{3}$≤2kπ+$\frac{π}{2}$,求得kπ-$\frac{π}{12}$≤x≤kπ+$\frac{5π}{12}$,
递增区间为[kπ-$\frac{π}{12}$,kπ+$\frac{5π}{12}$],k∈Z.
(2)在△ABC中,2acosC+c=2b,∴2a•$\frac{{a}^{2}{+b}^{2}{-c}^{2}}{2ab}$+c=2b,即b2+c2-a2=bc,
∴cosA=$\frac{{b}^{2}{+c}^{2}{-a}^{2}}{2bc}$=$\frac{1}{2}$,∴A=$\frac{π}{3}$.
∴0<B<$\frac{2π}{3}$,-$\frac{π}{3}$<2B-$\frac{π}{3}$<π,∴sin(2B-$\frac{π}{3}$)∈(-$\frac{\sqrt{3}}{2}$,1],
可得f(B)∈(1,$3+\sqrt{3}$].
点评 本题主要考查三角恒等变换,正弦函数的周期性和单调性,余弦定理、正弦函数的定义域和值域,属于中档题.

 轻松暑假总复习系列答案
轻松暑假总复习系列答案| A. | $\frac{x^2}{2}+{y^2}=1$ | B. | (x-1)2+y2=1 | C. | y=x2 | D. | x2-y2=1 |
| A. | f(a)<0,f(b)<0 | B. | f(a)>0,f(b)>0 | C. | f(a)>0,f(b)<0 | D. | f(a)<0,f(b)>0 |
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
(1)根据以上数据列出2×2列联表.
(2)能否在犯错误的概率不超过0.001的前提下认为40岁以上的人患胃病和生活规律有关系?
参考公式与临界值表:${K_{\;}}^2=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$
| P(K2≥k0) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| ko | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
| A. | y2=16x | B. | y2=8x | C. | y2=4x | D. | y2=2x |
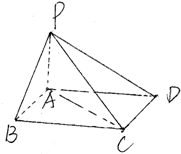 如图四棱锥P-ABCD中,底面ABCD为平行四边形,∠ABC=60°,PA=AB=1,BC=2,PA⊥底面ABCD
如图四棱锥P-ABCD中,底面ABCD为平行四边形,∠ABC=60°,PA=AB=1,BC=2,PA⊥底面ABCD