题目内容
已知长方体ABCD-A1B1C1D1中，AB=
，BC=BB1=1，求点D和点B到平面ACD1的距离.
解析：设BD与AC相交于O，作DE⊥AC，垂足为E，连结D1E，作DF⊥D1E，垂足为F.
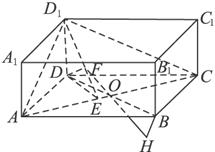
∵D1D⊥AC，DE⊥AC，
∴AC⊥平面 D1DE，DF
平面D1DE.∴AC⊥DF.
又∵DF⊥D1E，∴DF⊥平面D1AC，
D到平面D1AC的距离为DF.
在Rt△ADC中，
DE=
=
.
同理，在Rt△D1DE中，
DF=
.
过B作BH⊥平面ACD1，垂足为H，则BH∥DF.
又∵DO=OB，∴BH=DF.
∴点B和点D到平面ACD1的距离都是
.
练习册系列答案
浙江名校名师金卷系列答案
相关题目
已知长方体ABCD-A1B1C1D1中，AB=2，BC=4，AA1=4，点M是棱D1C1的中点．
已知长方体ABCD-A1B1C1D1中，DA=DD1=1，
已知长方体ABCD-A1B1C1D1中，M、N分别是BB1和BC的中点，AB=4，AD=2，
如图，已知长方体ABCD-A1B1C1D1，AB=BC=1，BB1=2，连接B1C，过B点作B1C．已知长方体ABCD-A1B1C1D1，下列向量的数量积一定不为0的是（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|