题目内容
关于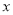 的不等式
的不等式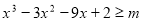 对
对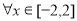 恒成立,则
恒成立,则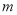 的取值范围( ).
的取值范围( ).
A. B.
B.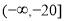 C.
C. D.[-12,7]
D.[-12,7]
B
【解析】
试题分析:令 ,因为
,因为 恒成立,即
恒成立,即 同时
同时 ,所以需找到
,所以需找到 在
在 上的最小值,首先
上的最小值,首先 ,当
,当 时,
时,
 ,当
,当 时,
时, ,所以
,所以 的单调递增区间是
的单调递增区间是 ,单调递减区间是
,单调递减区间是 ,比较
,比较 ,所以当
,所以当 时,
时, 取得最小值
取得最小值 ,
, ,答案为B.
,答案为B.
考点:1.恒成立问题;2.导函数;3.求最值.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目

 ,直线
,直线 。
。 为何值时,直线
为何值时,直线 与圆C相切;
与圆C相切; 与圆C相交于A、B两点,且AB=
与圆C相交于A、B两点,且AB= 时,求直线
时,求直线 的方程。
的方程。 、
、 ,且
,且 ,则
,则 ,且
,且 的( )条件。
的( )条件。 ,计算可得
,计算可得 ,
, ,
, ,
, ,
, 推测当
推测当 时,有 .
时,有 . ,则
,则 的共轭复数
的共轭复数 在复平面内对应的点( ).
在复平面内对应的点( ). 上任取一点
上任取一点 ,过点
,过点 作
作 轴的垂线段
轴的垂线段 ,
, 为垂足,当点
为垂足,当点 在圆上运动时,设线段
在圆上运动时,设线段 的中点
的中点 的轨迹为
的轨迹为
 的轨迹
的轨迹 方程;
方程; 与轨迹
与轨迹 交于
交于 两点,当
两点,当 为何值时,
为何值时, ?
? 与直线
与直线 及
及 所围成的封闭图形的面积为( ).
所围成的封闭图形的面积为( ). B.
B. C.
C. D.
D.
 ,且
,且 在
在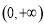 上单调递增.
上单调递增. 的值,并写出相应的函数
的值,并写出相应的函数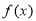 的解析式;
的解析式;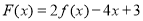 在区间
在区间 上不单调,求实数
上不单调,求实数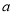 的取值范围;
的取值范围; ,使函数
,使函数 在区间
在区间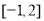 上的值域为
上的值域为 .若存在,求出
.若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.