题目内容
在圆 上任取一点
上任取一点 ,过点
,过点 作
作 轴的垂线段
轴的垂线段 ,
, 为垂足,当点
为垂足,当点 在圆上运动时,设线段
在圆上运动时,设线段 的中点
的中点 的轨迹为
的轨迹为
(1)写出点 的轨迹
的轨迹 方程;
方程;
(2)设直线 与轨迹
与轨迹 交于
交于 两点,当
两点,当 为何值时,
为何值时, ?
?
(1) ;(2)
;(2) .
.
【解析】
试题分析:(1)根据题意设 则
则 ,因为点
,因为点 为
为 的中点,所以由:
的中点,所以由: 解得:
解得: ,又因为点
,又因为点 在圆
在圆 上,所以
上,所以 即:
即: 化简为:
化简为: 即为所求轨迹方程;(2)设
即为所求轨迹方程;(2)设 ,由直线方程
,由直线方程 和(1)中的椭圆方程
和(1)中的椭圆方程 联立,再利用韦达定理求得:
联立,再利用韦达定理求得: ,代入
,代入 ,得到关于
,得到关于 的方程,进而求得
的方程,进而求得 的值.
的值.
试题解析:(1)轨迹C的方程为 ;
;
(2) 联立整理得:
联立整理得:
 解得
解得
 又因为
又因为 所以
所以
解得 所以:
所以: .
.
考点:1.相关点法求动点的轨迹方程;2.韦达定理.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 与直线
与直线 互相垂直,则
互相垂直,则 的值为( )
的值为( ) B.
B.  C.
C. D.
D.
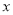 的不等式
的不等式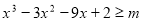 对
对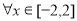 恒成立,则
恒成立,则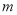 的取值范围( ).
的取值范围( ). B.
B.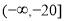 C.
C. D.[-12,7]
D.[-12,7]  的离心率为
的离心率为 ,则
,则 =( )
=( )  B.
B. C.
C. D.
D.
 ”拓展到空间,类比平面几何的上述结论,则正四面体内切球的半径等于这个正四面体高的 .
”拓展到空间,类比平面几何的上述结论,则正四面体内切球的半径等于这个正四面体高的 . 与双曲线
与双曲线 的公共焦点分别为
的公共焦点分别为 ,
, 为这两条曲线的一个交点,则
为这两条曲线的一个交点,则 的值为( ).
的值为( ). B.
B. C.
C. D.
D.
 ,
, ,若
,若 ,则
,则 ________.
________. ,
, ,
, ,则:( )
,则:( ) B.
B. C.
C. D.
D.