Question

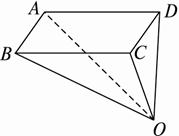
四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将△ABD沿对角线BD折起,记折起后点A的位置为P,且使平面PBD⊥平面BCD.

(1)求证:平面PBC⊥平面PDC;

(2)求二面角PBCD的大小.

Answer 1

(1)证明:折叠前:在四边形ABCD中,

∵AD∥BC,AD=AB,∠BAD=90°,

∴△ABD为等腰直角三角形.

又∵∠BCD=45°,

∴∠BDC=90°.

折叠后:∵面PBD⊥面BCD,CD⊥BD,

∴CD⊥面PBD.

又∵PB面PBD,

∴CD⊥PB.

又∵PB⊥PD,PD∩CD=D,

∴PB⊥面PDC.

又PB面PBC,故平面PBC⊥平面PDC.

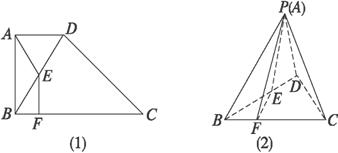
(2)解:在折叠前的四边形ABCD中,作AE⊥BD于点E,过点E作EF⊥BC于点F,

折叠后,AE⊥BD,EF⊥BC的位置关系不变.

∴PE⊥BD.

∵面PBD⊥面BCD,∴PE⊥平面BCD.

连结PF,∵EF⊥BC,∴PF⊥BC.

∴∠PFE为二面角PBCD的平面角.

在Rt△PEF中,由题设条件可解得tan∠PFE=.

故所求二面角的大小为arctan.