题目内容
已知函数f(x)=x2-|x|+a,若存在x1,x2,x3,x4(x1,x2,x3,x4互不相同),使f(x1)=f(x2)=f(x3)=f(x4)=1,则a的取值范围是 .
考点:二次函数的性质
专题:计算题,数形结合,函数的性质及应用
分析:在同一直角坐标系内画出直线y=1与曲线y=x2-|x|+a的图象,观察有四个交点的情况即可得到.
解答:
 解:如图,在同一直角坐标系内画出直线y=1与
解:如图,在同一直角坐标系内画出直线y=1与
曲线y=x2-|x|+a,
观图可知,a的取值必须满足
,
解得1<a<
.
故答案为:(1,
)
 解:如图,在同一直角坐标系内画出直线y=1与
解:如图,在同一直角坐标系内画出直线y=1与曲线y=x2-|x|+a,
观图可知,a的取值必须满足
|
解得1<a<
| 5 |
| 4 |
故答案为:(1,
| 5 |
| 4 |
点评:本小题主要考查函数的图象与性质、不等式的解法,着重考查了数形结合的数学思想.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
过原点且倾斜角为60°的直线被圆x2+y2-4y=0所截得的弦长为( )
A、2
| ||
| B、2 | ||
C、
| ||
D、
|
设集合P={0,1},那么集合P的子集个数是( )
| A、1 | B、2 | C、3 | D、4 |
要得到函数y=tan(x+
)的图象,只要将函数y=tanx的图象( )
| π |
| 6 |
A、向右平移
| ||
B、向左平移
| ||
C、向右平移
| ||
D、向左平移
|
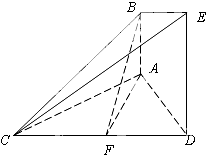 如图,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB,F为CD的中点.
如图,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB,F为CD的中点.