题目内容
已知函数f(x)=alnx+
x2-(1+a)x
(1)求函数f(x)的单调区间
(2)证明,当m,n∈N时,
m(m+n)[
+
+
+…+
]>n.
| 1 |
| 2 |
(1)求函数f(x)的单调区间
(2)证明,当m,n∈N时,
m(m+n)[
| 1 |
| ln(m+n) |
| 1 |
| ln(m+n-1) |
| 1 |
| ln(m+n-2) |
| 1 |
| ln(m+1) |
考点:利用导数求闭区间上函数的最值,利用导数研究函数的单调性
专题:计算题,证明题,导数的综合应用
分析:(1)由题意先求函数的定义域,再求导f′(x)=
+x-(1+a)=
,从而讨论导数的正负以确定函数的单调性;
(2)由(2)知,当a=-
时,f(x)=-
lnx+
x2-
x≥0;当且仅当x=1时,等号成立;从而可化出当>1时,
>
-
;从而证明.
| a |
| x |
| (x-1)(x-a) |
| x |
(2)由(2)知,当a=-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| lnx |
| 1 |
| x-1 |
| 1 |
| x |
解答:
解:(1)f(x)=alnx+
x2-(1+a)x的定义域为{x|x>0},
f′(x)=
+x-(1+a)=
;
①当a=1时,f′(x)≥0,f(x)在定义域上是增函数;
②当a>1时,1<x<a时,f′(x)<0,0<x<1或x>a时,f′(x)>0;
故f(x)的单调减区间为(1,a);单调增区间为(0,1),(a,+∞);
③当0<a<1时,a<x<1,f′(x)<0,0<x<a或x>1时,f′(x)>0;
故f(x)的单调减区间为(a,1);单调增区间为(0,a),(1,+∞);
④当a<0时,0<x<1,f′(x)<0,x>1时,f′(x)>0;
故f(x)的单调减区间为(0,1);单调增区间为(1,+∞);
(2)证明:由(2)知,
当a=-
时,f(x)=-
lnx+
x2-
x≥0;
当且仅当x=1时,等号成立;
即lnx≤x2-x,
当>1时,
>
-
;
故
+
+
+…+
>
-
+
-
+…+
-
=
-
=
;
故m(m+n)[
+
+
+…+
]>n.
| 1 |
| 2 |
f′(x)=
| a |
| x |
| (x-1)(x-a) |
| x |
①当a=1时,f′(x)≥0,f(x)在定义域上是增函数;
②当a>1时,1<x<a时,f′(x)<0,0<x<1或x>a时,f′(x)>0;
故f(x)的单调减区间为(1,a);单调增区间为(0,1),(a,+∞);
③当0<a<1时,a<x<1,f′(x)<0,0<x<a或x>1时,f′(x)>0;
故f(x)的单调减区间为(a,1);单调增区间为(0,a),(1,+∞);
④当a<0时,0<x<1,f′(x)<0,x>1时,f′(x)>0;
故f(x)的单调减区间为(0,1);单调增区间为(1,+∞);
(2)证明:由(2)知,
当a=-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
当且仅当x=1时,等号成立;
即lnx≤x2-x,
当>1时,
| 1 |
| lnx |
| 1 |
| x-1 |
| 1 |
| x |
故
| 1 |
| ln(m+n) |
| 1 |
| ln(m+n-1) |
| 1 |
| ln(m+n-2) |
| 1 |
| ln(m+1) |
>
| 1 |
| m+n-1 |
| 1 |
| m+n |
| 1 |
| m+n-2 |
| 1 |
| m+n-1 |
| 1 |
| m |
| 1 |
| m+1 |
=
| 1 |
| m |
| 1 |
| m+n |
| n |
| m(m+n) |
故m(m+n)[
| 1 |
| ln(m+n) |
| 1 |
| ln(m+n-1) |
| 1 |
| ln(m+n-2) |
| 1 |
| ln(m+1) |
点评:本题考查了导数的综合应用及构造函数证明不等式的方法应用,属于中档题.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
已知实数x,y满足不等式组
,则2x+y的最大值为( )
|
| A、3 | B、4 | C、6 | D、9 |
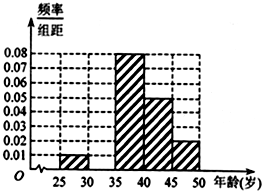 某市要对辖区内的中学教师的年龄进行调查,现从中随机抽出200名教师,已知抽到的教师年龄都在[25,50)岁之间,根据调查结果得出教师的年龄情况残缺的频率分布直方图如图所示,利用这个残缺的频率分布直方图估计该市辖区内中学教师的年龄的中位数大约是( )
某市要对辖区内的中学教师的年龄进行调查,现从中随机抽出200名教师,已知抽到的教师年龄都在[25,50)岁之间,根据调查结果得出教师的年龄情况残缺的频率分布直方图如图所示,利用这个残缺的频率分布直方图估计该市辖区内中学教师的年龄的中位数大约是( )| A、37.1岁 |
| B、38.1岁 |
| C、38.7岁 |
| D、43.1岁 |
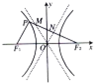 已知点P是双曲线C:
已知点P是双曲线C:| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||
B、
| ||
| C、2 | ||
D、
|
执行如图的程序框图,若判断框中填入“k>8”,则输出的S=( )


| A、11 | B、20 | C、28 | D、35 |
