题目内容
5.若x,y满足$\left\{\begin{array}{l}{x+y-3≥0}\\{kx-y+3≥0}\\{y≥0}\\{\;}\end{array}\right.$,且当z=y-x的最小值为-12,则k的值为( )| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | -$\frac{1}{4}$ |
分析 作出不等式组对应的平面区域,根据目标是的最小值建立不等式关系进行求解即可.
解答 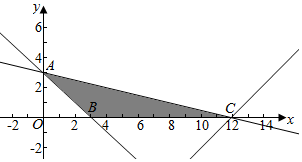 解:由z=y-x得y=x+z,
解:由z=y-x得y=x+z,
要使z=y-x的最小值为-12,
即y=x-12,
则不等式对应的区域在y=x-12的上方,
先作出$\left\{\begin{array}{l}{y≥0}\\{x+y-3≥0}\\{y=x-12}\end{array}\right.$对应的图象,
由$\left\{\begin{array}{l}{y=0}\\{y=x-12}\end{array}\right.$得$\left\{\begin{array}{l}{x=12}\\{y=0}\end{array}\right.$,即C(12,0),
同时C(12,0)也在直线kx-y+3=0上,
则12k+3=0,得k=-$\frac{1}{4}$,
故选:D.
点评 本题主要考查线性规划的应用,利用数形结合是解决本题的关键.

练习册系列答案
相关题目
15.已知$sin(x-\frac{9π}{14})cos\frac{π}{7}+cos(x-\frac{9π}{14})sin\frac{π}{7}=\frac{1}{3}$,则cosx等于( )
| A. | $\frac{1}{3}$ | B. | $-\frac{1}{3}$ | C. | $\frac{{2\sqrt{2}}}{3}$ | D. | $±\frac{{2\sqrt{2}}}{3}$ |
16.由不等式$\left\{\begin{array}{l}0≤x≤1\\ 0≤y≤1\end{array}\right.$确定的平面区域记为Ω1,不等式$\left\{\begin{array}{l}{(x-\frac{1}{2})^2}+{(y-\frac{1}{2})^2}≤\frac{1}{2}\;\;\\ x≥y\\ x+y≥1\\ \;\;\end{array}\right.$确定的平面区域记为Ω2,在Ω1中随机取一点,则该点恰好在Ω2内的概率为( )
| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{8}$ |
13.若复数z满足z(2-i)=10+5i(i为虚数单位),则|z|=( )
| A. | 25 | B. | 10 | C. | 5 | D. | $\sqrt{5}$ |
20.将函数f(x)=sin(2x+φ)+$\sqrt{3}$cos(2x+φ )(0<φ<π)的图象向左平移$\frac{π}{4}$个单位后,得到函数的图象关于点{$\frac{π}{2}$,0}对称,则φ等于( )
| A. | -$\frac{π}{6}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{3}$ |
17.设集合A={x|4x2≤1},B={x|lnx<0},则A∩B=( )
| A. | $(-\frac{1}{2},\frac{1}{2})$ | B. | $(0,\frac{1}{2})$ | C. | $[\frac{1}{2},1)$ | D. | $(0,\frac{1}{2}]$ |
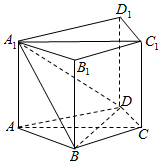 如图,在直四棱柱ABCD-A1B1C1D1中,∠BAD=60°,AB=BD,BC=CD.
如图,在直四棱柱ABCD-A1B1C1D1中,∠BAD=60°,AB=BD,BC=CD.