题目内容
8.已知x,lga,lgb,y成等差数列,a>1,b>1,且a+b=20,则x+y的最大值为2.分析 由对数的运算和等差数列可得x+y=lga+lgb=lgab≤lg($\frac{a+b}{2}$)2=lg100=2,验证等号成立即可.
解答 解:∵x,lga,lgb,y成等差数列,a>1,b>1,且a+b=20,
∴x+y=lga+lgb=lgab≤lg($\frac{a+b}{2}$)2=lg100=2,
当且仅当a=b=10时取等号.
∴x+y的最大值为2,
故答案为:2.
点评 本题考查基本不等式求最值,涉及对数的运算和等差数列,属基础题.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
13.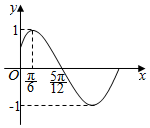 已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则$\sum_{n=1}^{2016}$f($\frac{nπ}{6}$)=( )
已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则$\sum_{n=1}^{2016}$f($\frac{nπ}{6}$)=( )
 已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则$\sum_{n=1}^{2016}$f($\frac{nπ}{6}$)=( )
已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则$\sum_{n=1}^{2016}$f($\frac{nπ}{6}$)=( )| A. | -1 | B. | $\frac{1}{2}$ | C. | 1 | D. | 0 |
3.已知x,y是实数,则“x>1,y<1”是“(x-1)(y-1)<0”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
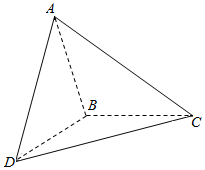 三棱锥A-BCD中,平面ABC⊥平面BCD,AB=BC=BD,∠ABC=∠DBC=120°,则二面角A-BD-C的平面角的正切值是-2.
三棱锥A-BCD中,平面ABC⊥平面BCD,AB=BC=BD,∠ABC=∠DBC=120°,则二面角A-BD-C的平面角的正切值是-2.