题目内容
9.若复数z=$\frac{a+3i}{i}$+a的实部为2,则复数z的虚部是( )| A. | -i | B. | -3 | C. | 1 | D. | 2 |
分析 由条件利用两个复数代数形式的运算法则求得a的值,再利用复数的基本概念求得它的虚部.
解答 解:∵复数z=$\frac{a+3i}{i}$+a=a+3-ai的实部为2,∴a+3=2,∴a=-1,
∴复数z的虚部是-a=1,
故选:C.
点评 本题主要考查两个复数代数形式的运算,复数的基本概念,属于基础题.

练习册系列答案
相关题目
2.下列各式恒成立的是( )
| A. | tan$\frac{α}{2}$=$\frac{1-cosα}{sinα}$ | B. | $\frac{1+cos2α}{2}$=cos2α | ||
| C. | $\frac{2tan\frac{α}{2}}{1-ta{n}^{2}\frac{α}{2}}$=tanα | D. | ±$\sqrt{\frac{1-cosα}{1+cosα}}$=tan$\frac{α}{2}$ |
19.下列函数f(x)与g(x)是相同函数的是( )
| A. | f(x)=$\frac{x-1}{{x}^{2}-1}$,g(x)=$\frac{1}{1+x}$ | B. | f(x)=($\sqrt{x}$)2,g(x)=$\sqrt{{x}^{2}}$ | ||
| C. | f(x)=$\root{3}{{x}^{4}-{x}^{3}}$,g(x)=x$\root{3}{x-1}$ | D. | f(x)=1,g(x)=sin(arcsinx) |
14.若实数x、y满足$\left\{\begin{array}{l}{{x}^{2}+{y}^{2}≤1}\\{2x-y≥0}\end{array}\right.$,则z=x+y的最大值是( )
| A. | $\frac{3\sqrt{5}}{5}$ | B. | $\frac{\sqrt{5}}{5}$ | C. | $\sqrt{2}$ | D. | 1 |
1.矩形ABCD中,AB=2$\sqrt{3}$,AD=2,点E、F分别为线段BC、CD边上的动点,且满足EF=1,则$\overrightarrow{AE}$$•\overrightarrow{AF}$的最小值是( )
| A. | 12 | B. | 16 | C. | 20 | D. | 24 |
18.函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则( )
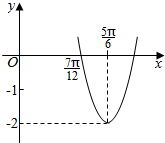

| A. | 函数f(x)在区间[0,$\frac{π}{2}$]上单调递增 | B. | 函数f(x)在区间[0,$\frac{π}{2}$]上单调递减 | ||
| C. | 函数f(x)在区间[0,$\frac{π}{2}$]上的最小值为-2 | D. | 函数f(x)在区间[0,$\frac{π}{2}$]上的最小值为-1 |