题目内容
(12分)已知椭圆C: 以双曲线
以双曲线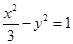 的焦点为顶点,其离心率与双曲线的离心率互为倒数.
的焦点为顶点,其离心率与双曲线的离心率互为倒数.
(1)求椭圆C的方程;
(2)若椭圆C的左、右顶点分别为点A,B,点M是椭圆C上异于A,B的任意一点.
①求证:直线MA,MB的斜率之积为定值;
②若直线MA,MB与直线x=4分别交于点P,Q,求线段PQ长度的最小值.
 以双曲线
以双曲线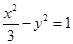 的焦点为顶点,其离心率与双曲线的离心率互为倒数.
的焦点为顶点,其离心率与双曲线的离心率互为倒数.(1)求椭圆C的方程;
(2)若椭圆C的左、右顶点分别为点A,B,点M是椭圆C上异于A,B的任意一点.
①求证:直线MA,MB的斜率之积为定值;
②若直线MA,MB与直线x=4分别交于点P,Q,求线段PQ长度的最小值.
(1)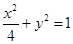 (2)①证明见解析②
(2)①证明见解析②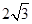
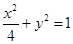 (2)①证明见解析②
(2)①证明见解析②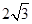
试题分析:(1)易知双曲线
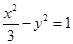 的焦点为(-2,0),(2,0),离心率为
的焦点为(-2,0),(2,0),离心率为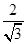 ,……2分
,……2分则在椭圆C中a=2,e=
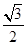 ,
,故在椭圆C中c=
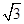 ,b=1,所以椭圆C的方程为
,b=1,所以椭圆C的方程为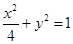 ……4分
……4分(2)①设M(x0,y0)(x0≠±2),由题易知A(-2,0),B(2,0),
则kMA=
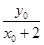 ,kMB=
,kMB=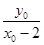 ,故kMA·kMB=
,故kMA·kMB=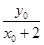
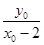 =
=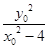 , ……6分
, ……6分点M在椭圆C上,则
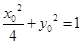 ,即
,即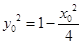
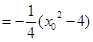 ,
,故kMA·kMB=
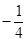 ,即直线MA,MB的斜率之积为定值。 ……8分
,即直线MA,MB的斜率之积为定值。 ……8分②解法一:设P(4,y1),Q(4,y2),则kMA=kPA=
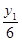 ,kMB=kBQ=
,kMB=kBQ=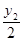 ,……9分
,……9分由①得
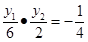 ,即y1y2=-3,当y1>0,y2<0时,|PQ|=|y1-y2|≥2
,即y1y2=-3,当y1>0,y2<0时,|PQ|=|y1-y2|≥2 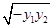 =
=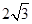 ,当且仅当y1=
,当且仅当y1=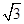 ,y2=-
,y2=-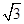 时等号成立.……11分
时等号成立.……11分同理,当y1<0,y2>0时,当且仅当
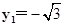 ,y2=
,y2=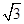 时,|PQ|有最小值
时,|PQ|有最小值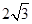 . ……12分
. ……12分解法二:设直线MA的斜率为k,则直线MA的方程为y=k(x+2),从而P(4,6k) ……9分
由①知直线MB的斜率为
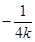 ,则直线MB的方程为y=
,则直线MB的方程为y=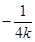 (x-2),
(x-2),故得
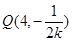 ,故
,故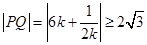 ,当且仅当
,当且仅当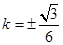 时等号成立,
时等号成立,即|PQ|有最小值
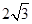 . ……12分
. ……12分点评:直线与圆锥曲线位置关系的题目是每年高考必考的题目,且一般都以压轴题的形式出现,所以难度较大,关键是运算量比较大,要尽量应用数形结合简化运算,还要细心求解.

练习册系列答案
相关题目
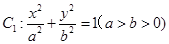 的右焦点为F,上顶点为A,P为C
的右焦点为F,上顶点为A,P为C 上任一点,MN是圆
上任一点,MN是圆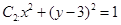 的一条直径,若与AF平行且在y轴上的截距为
的一条直径,若与AF平行且在y轴上的截距为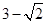 的直线
的直线 恰好与圆
恰好与圆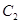 相切.
相切.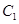 的离心率;
的离心率;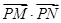 的最大值为49,求椭圆C
的最大值为49,求椭圆C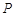 是椭圆
是椭圆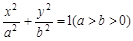 上的一动点,且
上的一动点,且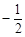 ,则椭圆离心率为
,则椭圆离心率为 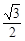
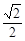
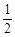
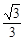
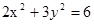 有两个交点 ( )
有两个交点 ( )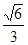 <k<
<k<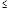 k
k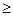
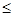 —
—
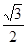

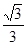
 是椭圆E:
是椭圆E: 的左右焦点,P在直线
的左右焦点,P在直线 上一点,
上一点,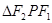 是底角为
是底角为 的等腰三角形,则椭圆E的离心率为( )
的等腰三角形,则椭圆E的离心率为( )



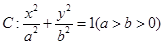 的离心率为
的离心率为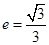 ,以原点为圆心,椭圆短半轴长为半径的圆与直线
,以原点为圆心,椭圆短半轴长为半径的圆与直线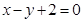 相切,
相切,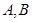 分别是椭圆的左右两个顶点,
分别是椭圆的左右两个顶点,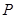 为椭圆
为椭圆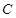 上的动点.
上的动点.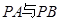 的斜率分别为
的斜率分别为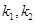 ,求
,求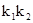 的值。
的值。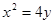 焦点的直线依次交抛物线与圆
焦点的直线依次交抛物线与圆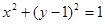 于点A、B、C、D,则
于点A、B、C、D,则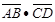 的值是( )
的值是( )
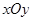 中,点
中,点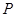 到两点
到两点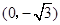 ,
,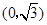 的距离之和等于
的距离之和等于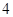 ,设点
,设点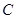 。
。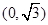 作两条互相垂直的直线
作两条互相垂直的直线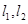 分别与曲线
分别与曲线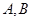 和
和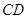 。
。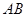 为直径的圆过能否过坐标原点,若能求出此时的
为直径的圆过能否过坐标原点,若能求出此时的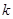 值,若不能说明理由;
值,若不能说明理由;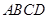 面积的取值范围。
面积的取值范围。