题目内容
k为何值时,直线y=kx+2和椭圆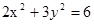 有两个交点 ( )
有两个交点 ( )
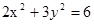 有两个交点 ( )
有两个交点 ( )A.—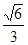 <k< <k<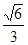 | B.k>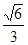 或k< — 或k< —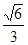 |
C.—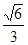 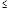 k k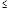 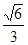 | D.k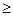 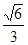 或k 或k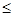 — —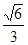 |
B
试题分析:由
 可得 :(2+3k2)x2+12kx+6=0,由△=144k2-24(2+3k2)>0得k>
可得 :(2+3k2)x2+12kx+6=0,由△=144k2-24(2+3k2)>0得k>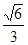 或k< —
或k< —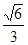 ,此时直线和椭圆有两个公共点。
,此时直线和椭圆有两个公共点。点评:判断直线和椭圆交点个数的主要方法,联立方程组,消元,判断△>0、△=0还是△<0。

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
 以双曲线
以双曲线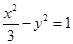 的焦点为顶点,其离心率与双曲线的离心率互为倒数.
的焦点为顶点,其离心率与双曲线的离心率互为倒数. 在曲线
在曲线 上,点
上,点 在曲线
在曲线 上,则
上,则 的最小值等于 .
的最小值等于 .
 的焦点F恰好是曲线
的焦点F恰好是曲线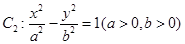 的右焦点,且
的右焦点,且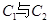 交点的连线过点F,则曲线
交点的连线过点F,则曲线 的离心率为
的离心率为
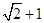


 经过点
经过点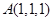 ,且
,且 是它的一个法向量. 类比曲线方程的定义以及求曲线方程的基本步骤,可求得平面
是它的一个法向量. 类比曲线方程的定义以及求曲线方程的基本步骤,可求得平面 的焦点是双曲线C的一个焦点,且双曲线经过点
的焦点是双曲线C的一个焦点,且双曲线经过点 ,又知直线
,又知直线 与双曲线C相交于A、B两点.
与双曲线C相交于A、B两点.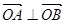 ,求实数k值.
,求实数k值.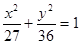 有相同焦点,且经过点
有相同焦点,且经过点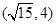 ,
,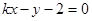 与曲线
与曲线 有两个不同的交点,则实数
有两个不同的交点,则实数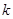 的取值范围是( )
的取值范围是( )



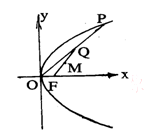
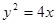 ,焦点为
,焦点为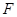 ,顶点为
,顶点为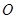 ,点
,点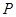 在抛物线上移动,
在抛物线上移动,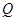 是
是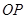 的中点,
的中点,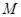 是
是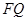 的中点,求点
的中点,求点