题目内容
（Ⅰ） 计算：2log2
-(
)-
+lg
+(
-1)lg1；
（Ⅱ）已知函数f(x)=
，若f(2x)=
，求(
)x的值．
| 1 |
| 4 |
| 8 |
| 27 |
| 2 |
| 3 |
| 1 |
| 100 |
| 2 |
（Ⅱ）已知函数f(x)=
| 2x+1 |
| 2x-1 |
| 5 |
| 4 |
| 2 |
分析：（Ⅰ）利用对数运算法则即可求解；
（Ⅱ）先由f(2x)=
求出2x值，再由此即可求出答案．
（Ⅱ）先由f(2x)=
| 5 |
| 4 |
解答：解：（Ⅰ）原式=
-
-2+1=-3．
（Ⅱ）由f(2x)=
，得
=
，
∴22x=9，∴，2x=3，
∴(
)x=(2x)
=
．
| 1 |
| 4 |
| 9 |
| 4 |
（Ⅱ）由f(2x)=
| 5 |
| 4 |
| 22x+1 |
| 22x-1 |
| 5 |
| 4 |
∴22x=9，∴，2x=3，
∴(
| 2 |
| 1 |
| 2 |
| 3 |
点评：本题考查对数运算法则及有理数指数幂的运算，属基础题．
练习册系列答案
举一反三期末百分冲刺卷系列答案
相关题目
如图，A、B两点在河的两岸，一测量者在A的同侧，在所在的河岸边选定一点C，测出AC的距离为20m，∠ACB=60°，∠CAB=75°后，可以计算出A、B两点的距离为（ ）计算：∫-22|x3-1|dx=（ ）
| A、0 | ||
| B、-4 | ||
C、
| ||
| D、16 |
）
-9.60+（3
）
+
2-log5
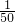-log514．
）
-9.6+（3
）
+
2-log5
-log514．