题目内容
1.已知圆C:(x-1)2+(y-2)2=25,直线l:(2m+1)x+(m+1)y-7m-4=0,若直线l被圆C截得的弦长最短,则m的值为-$\frac{3}{4}$.分析 由于直线过定点M(3,1),点M在圆C:(x-1)2+(y-2)2=25的内部,故直线被圆截得的弦长最短时,CM垂直于直线l,根据它们的斜率之积等于-1求出m的值.
解答 解:直线l:(2m+1)x+(m+1)y-7m-4=0 即(x+y-4)+m(2x+y-7)=0,过定点M(3,1),
由于点M在圆C:(x-1)2+(y-2)2=25的内部,故直线被圆截得的弦长最短时,CM垂直于直线l,
故它们的斜率之积等于-1,即$\frac{1-2}{3-1}×(-\frac{2m+1}{m+1})$=-1,解得m=-$\frac{3}{4}$,
故答案为:-$\frac{3}{4}$.
点评 本题主要考查直线和圆的位置关系,直线过定点问题,属于基础题.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
16.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$与抛物线y2=4x的交点为A,B,且直线AB过双曲线与抛物线的公共焦点F,则双曲线的实轴长为( )
| A. | $\sqrt{2}$+1 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$-1 | D. | 2$\sqrt{2}$-2 |
6.若角α的终边与单位圆的交点为$P(\frac{12}{13},-\frac{5}{13})$,则tanα=( )
| A. | $\frac{5}{12}$ | B. | $-\frac{5}{12}$ | C. | $-\frac{12}{5}$ | D. | $\frac{12}{5}$ |
13.已知函数f(x)是定义在R上的偶函数,当x≥0时,$f(x)=\left\{\begin{array}{l}\frac{3}{2}cos\frac{π}{2}(1-x),0≤x≤1\\{(\frac{1}{2})^x}+1,x>1\end{array}\right.$,若函数g(x)=5[f(x)]2-(5a+6)f(x)+6a(a∈R)有且仅有6个不同的零点,则实数a的取值范围( )
| A. | $(0,1]∪\left\{{\frac{3}{2}}\right\}$ | B. | $(0,\frac{3}{2}]$ | C. | $(0,1)∪\left\{{\frac{3}{2}}\right\}$ | D. | $(0,\frac{3}{2})∪\left\{0\right\}$ |
10.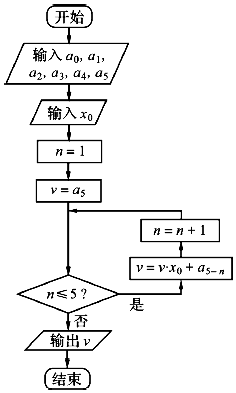 执行如图所示的程序框图,若输入a0=0,a1=1,a2=2,a3=3,a4=4,a5=5,x0=-1,则输出v的值为( )
执行如图所示的程序框图,若输入a0=0,a1=1,a2=2,a3=3,a4=4,a5=5,x0=-1,则输出v的值为( )
 执行如图所示的程序框图,若输入a0=0,a1=1,a2=2,a3=3,a4=4,a5=5,x0=-1,则输出v的值为( )
执行如图所示的程序框图,若输入a0=0,a1=1,a2=2,a3=3,a4=4,a5=5,x0=-1,则输出v的值为( )| A. | 15 | B. | 3 | C. | -3 | D. | -15 |
 如图,在边长是2的正方体ABCD-A1B1C1D1中,E,F分别为AB,A1C的中点.
如图,在边长是2的正方体ABCD-A1B1C1D1中,E,F分别为AB,A1C的中点.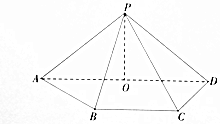 如图,四棱锥P-ABCD中,O为AD的中点,AD∥BC,CD⊥平面PAD,PA=PD=5.
如图,四棱锥P-ABCD中,O为AD的中点,AD∥BC,CD⊥平面PAD,PA=PD=5.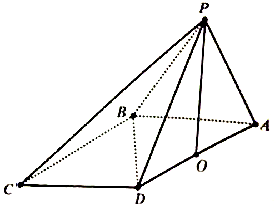 在四棱锥P-ABCD中,$∠DBA=\frac{π}{2}$,$AB\underline{\underline∥}CD$,△PAB和△PBD都是边长为2的等边三角形,设P在底面ABCD的射影为O.
在四棱锥P-ABCD中,$∠DBA=\frac{π}{2}$,$AB\underline{\underline∥}CD$,△PAB和△PBD都是边长为2的等边三角形,设P在底面ABCD的射影为O.