题目内容
11.设集合L={l|直线l与直线y=2x相交,且以交点的横坐标为斜率},若点(-2,2)到集合L中直线l的距离最小,则直线l的方程是y=0.分析 设直线l与直线y=2x相交于E(t,2t).可得直线l的方程为:y-2t=t(x-t).利用点到直线的距离公式可得点(-2,2)到直线l的距离d.通过变形利用基本不等式即可得出结论.
解答 解:设直线l与直线y=2x相交于E(t,2t).
则直线l的方程为:y-2t=t(x-t),化为tx-y+2t-t2=0.
点(-2,2)到直线l的距离d=$\frac{|-2t-2+2t-{t}^{2}|}{\sqrt{{t}^{2}+1}}$=$\sqrt{{t}^{2}+1}$+$\frac{1}{\sqrt{{t}^{2}+1}}$≥2,当且仅当t=0时取等号.
∴直线l的方程是y=0.
故答案为:y=0.
点评 本题考查了直线的交点、点到直线的距离公式、基本不等式的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
13. 一个几何体的三视图如图所示,该几何体外接球的表面积为( )
一个几何体的三视图如图所示,该几何体外接球的表面积为( )
 一个几何体的三视图如图所示,该几何体外接球的表面积为( )
一个几何体的三视图如图所示,该几何体外接球的表面积为( )| A. | 36π | B. | $\frac{112}{3}π$ | C. | 32π | D. | 28π |
3.已知函数f(x)=x2ex+lnt-a,若对任意的t∈[1,e],f(x)在区间[-1,1]总存在唯一的零点,则实数a的取值范围是( )
| A. | [1,e] | B. | $(1+\frac{1}{e},e]$ | C. | (1,e] | D. | $[1+\frac{1}{e},e]$ |
 ,则当
,则当 且
且 时,求
时,求 的解析式;
的解析式; 是一次函数,且满足
是一次函数,且满足 ,求
,求 的解析式.
的解析式. 满足
满足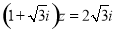 (
(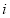 为虚数单位),则
为虚数单位),则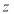 在复平面内对应的点位于( )
在复平面内对应的点位于( ) 如图,在四棱椎P-ABCD中,侧棱PD⊥底面ABCD,底面ABCD为梯形,AB∥CD,∠BAD=∠ADC=90°,DC=2AB=2,DA=PD=$\sqrt{3}$,E为BC的中点,连结AE,交BD于点O.
如图,在四棱椎P-ABCD中,侧棱PD⊥底面ABCD,底面ABCD为梯形,AB∥CD,∠BAD=∠ADC=90°,DC=2AB=2,DA=PD=$\sqrt{3}$,E为BC的中点,连结AE,交BD于点O.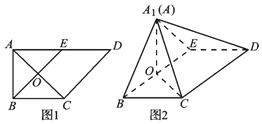 如图1,在直角梯形ABCD中,AD∥BC,∠BAD=$\frac{π}{2}$,AB=BC=1,AD=2,E是AD的中点,O是AC与BE的交点.将△ABE沿BE折起到图22中△A1BE的位置,得到四棱锥A1-BCDE.
如图1,在直角梯形ABCD中,AD∥BC,∠BAD=$\frac{π}{2}$,AB=BC=1,AD=2,E是AD的中点,O是AC与BE的交点.将△ABE沿BE折起到图22中△A1BE的位置,得到四棱锥A1-BCDE. 在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD是一直角梯形,∠BAD=90°,AD∥BC,AB=BC=a,PA=$\frac{{2\sqrt{3}}}{3}$a,AD=2a.
在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD是一直角梯形,∠BAD=90°,AD∥BC,AB=BC=a,PA=$\frac{{2\sqrt{3}}}{3}$a,AD=2a.