题目内容
圆(x-
)2+(y+1)2=
关于直线x-y+1=0对称的圆的方程是 .
| 1 |
| 2 |
| 5 |
| 4 |
考点:圆的标准方程
专题:直线与圆
分析:设圆心(
,-1)关于直线x-y+1=0对称的点的坐标为(m,n),利用垂直以及中点在轴上,求得m,n的值,可得对称圆的方程.
| 1 |
| 2 |
解答:
解:设圆心(
,-1)关于直线x-y+1=0对称的点的坐标为(m,n),
则由
求得
,故对称圆的圆心为(-2,
),对称圆的半径和原来的圆一样,
故对称圆的方程为(x+2)2+(y-
)2=
,
故答案为:(x+2)2+(y-
)2=
.
| 1 |
| 2 |
则由
|
|
| 3 |
| 2 |
故对称圆的方程为(x+2)2+(y-
| 3 |
| 2 |
| 5 |
| 4 |
故答案为:(x+2)2+(y-
| 3 |
| 2 |
| 5 |
| 4 |
点评:本题主要考查直线和圆的位置关系,求一个圆关于直线的对称圆的方程的方法,关键是求出圆心关于直线的对称点的坐标,属于基础题.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
(
-
)15的展开式中,不含a的项是第( )项.
| 3 | a |
| 1 | ||
|
| A、6项 | B、8项 | C、9项 | D、7项 |
已知点A(3,6),B(2,4),则直线AB的斜率是( )
| A、1 | B、2 | C、3 | D、4 |
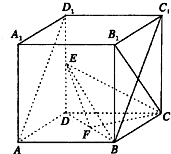 如图所示,在棱长为1的正方体AC1中,E,F分别为DD1,DB的中点.
如图所示,在棱长为1的正方体AC1中,E,F分别为DD1,DB的中点.