题目内容
18.函数$f(x)=4{sin^2}\frac{x}{2}sin({x-\frac{π}{2}})+2cosx-1-|{lg({x+1})}|$的零点个数为( )| A. | 5 | B. | 6 | C. | 7 | D. | 9 |
分析 利用诱导公式以及二倍角公式化简函数的解析式,考查两个函数的图象,频道零点个数即可.
解答 解:函数$f(x)=4{sin^2}\frac{x}{2}sin({x-\frac{π}{2}})+2cosx-1-|{lg({x+1})}|$
=2cosx(1-2sin2$\frac{x}{2}$)-1-|lg(x+1)|
=2cos2x-1-|lg(x+1)|
=cos2x-|lg(x+1)|.
函数$f(x)=4{sin^2}\frac{x}{2}sin({x-\frac{π}{2}})+2cosx-1-|{lg({x+1})}|$的零点,就是cos2x-|lg(x+1)|=0的根.
即:y=cos2x,与y=|lg(x+1)|解得的个数.
如图: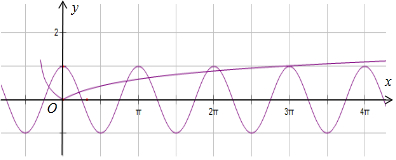
lg|3π+1|>lg10=1,
两个函数的图象的交点有6个.
故选:B.
点评 本题考查函数的零点个数的判断,数形结合思想的应用,考查转化思想以及计算能力.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
8.已知复数$z=3+\frac{3-4i}{4+3i}$,则$\overline z$=( )
| A. | 3+5i | B. | 3+i | C. | 3-i | D. | 3-5i |
9.已知f1(x)=sinx+cosx,fn+1(x)是fn(x)的导函数,即f2(x)=f1′(x),f3(x)=f2′(x),…,fn+1(x)=fn′(x),n∈N*,则f2017(x)=( )
| A. | sinx+cosx | B. | sinx-cosx | C. | -sinx+cosx | D. | -sinx-cosx |
10.定义在R上的偶函数f(x)满足f(1-x)=f(1+x),当x∈[1,2]时,f(x)=lnx.则直线x-5y+3=0与曲线y=f(x)的交点个数为(参考数据:ln2≈0.69,ln3≈1.10)( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
16.在△ABC中角A,B,C所对的边分别为a,b,c,满足ccosB+(b-2a)cosC=0.且c=2$\sqrt{3}$
(1)求角C的大小;
(2)求△ABC面积最大值,并判断此时△ABC的形状.
(1)求角C的大小;
(2)求△ABC面积最大值,并判断此时△ABC的形状.
17.设a,b,c∈R且a>b,则下列选项中正确的是( )
| A. | ac>bc | B. | a2>b2 | C. | a3>b3 | D. | $\frac{1}{a}>\frac{1}{b}$ |