题目内容
16.设椭圆$\frac{x^2}{m}+\frac{y^2}{3}=1$的两个焦点F1,F2都在x轴上,P是第一象限内该椭圆上的一点,且$\frac{{sin∠P{F_1}{F_2}+sin∠P{F_2}{F_1}}}{{sin∠{F_1}P{F_2}}}=2$,则正数m的值为4.分析 由椭圆$\frac{x^2}{m}+\frac{y^2}{3}=1$的两个焦点F1,F2都在x轴上,得m>3,正弦定理得:$\frac{|P{F}_{2}|+|P{F}_{1}|}{|{F}_{1}{F}_{2}|}$=$\frac{2a}{2c}$=2,由此能求出m.
解答 解:∵椭圆$\frac{x^2}{m}+\frac{y^2}{3}=1$的两个焦点F1,F2都在x轴上,∴m>3,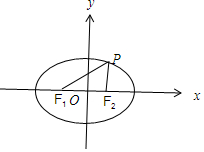
∵P是第一象限内该椭圆上的一点,且$\frac{{sin∠P{F_1}{F_2}+sin∠P{F_2}{F_1}}}{{sin∠{F_1}P{F_2}}}=2$,
∴由正弦定理得:$\frac{|P{F}_{2}|+|P{F}_{1}|}{|{F}_{1}{F}_{2}|}$=$\frac{2a}{2c}$=2,
∴e=$\frac{c}{a}=\frac{\sqrt{m-3}}{\sqrt{m}}$=$\frac{1}{2}$,
解得m=4.
故答案为:4.
点评 本题考查正数值的求法,考查椭圆、离心率、正弦定理等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.下列函数中,既是偶函数又在区间[0,+∞)上单调递减的是( )
| A. | y=x3 | B. | y=ln|x| | C. | y=sin($\frac{π}{2}$-x) | D. | y=-x2-1 |
8.复数z=-1+2i,则z在复平面内对应的点所在象限为( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
17.某地物价部门对该地的5家商场的某商品一天的销售量及其价格进行调查,5家商场该商品的售价x元和销售量y件之间的一组数据如表所示,由散点图知,销售量y与价格x之间有较好的线性相关关系,其线性回归直线方程是$\stackrel{∧}{y}$=-3.2x+$\stackrel{∧}{a}$,则$\stackrel{∧}{a}$值为( )
| 价格x(元) | 9 | 9.5 | 10 | 10.5 | 11 |
| 销售量y(件) | 11 | 10 | 8 | 6 | 5 |
| A. | 30 | B. | 40 | C. | 45 | D. | 50 |
 如图,直三棱柱ABC-A1B1C1中,AB=AC=AA1,AB⊥AC,M是CC1的中点,N是BC的中点,点P在线段A1B1上运动.
如图,直三棱柱ABC-A1B1C1中,AB=AC=AA1,AB⊥AC,M是CC1的中点,N是BC的中点,点P在线段A1B1上运动. 阅读程序框图,并完成下列问题:
阅读程序框图,并完成下列问题: