题目内容
12.已知命题p1:函数y=ex-e-x在R为增函数,p2:函数y=ex+e-x在(0,1)为减函数.则命题p1∧p2;p1∨p2;p1∧¬p2;¬p1∨p2中真命题的个数为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据指数函数,复合函数,对勾函数的图象和性质,分析命题p1,p2的真假,进而根据复合命题,真假判断的真值表,得到答案.
解答 解:函数y=ex在R为增函数,函数y=e-x在R为减函数,
故函数y=ex-e-x在R为增函数,
即命题p1为真命题,
令t=ex,由x∈(0,1)得:t∈(1,e),
y=ex+e-x=t+$\frac{1}{t}$,
由对勾函数的图象和性质得:y=t+$\frac{1}{t}$,t∈(1,e)为增函数,
t=ex,也为增函数,
故y=ex+e-x,x∈(0,1)为增函数,
故命题p2为假命题,
故命题p1∧p2为假命题;
p1∨p2为真命题;
p1∧¬p2为真命题;
¬p1∨p2为假命题,
故选:B
点评 本题以命题的真假判断与应用为载体,考查了复合命题,指数函数,复合函数,对勾函数的图象和性质,难度中档.

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
7.椭圆my2+x2=1的一个顶点在抛物线$y=\frac{1}{2}{x^2}$的准线上,则椭圆的离心率( )
| A. | $\frac{{\sqrt{63}}}{8}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | 4 | D. | $\frac{{\sqrt{5}}}{2}$ |
4.若两个不同平面α、β的法向量分别为$\overrightarrow{u}$=(1,2,-1),$\overrightarrow{v}$=(-2,2,2),则( )
| A. | α、β相交但不垂直 | B. | α⊥β | C. | α∥β | D. | 以上均不正确 |
 已知某四棱锥的三视图如图所示,则该几何体的各侧面中,面积的最小值为$\frac{1}{2}$.
已知某四棱锥的三视图如图所示,则该几何体的各侧面中,面积的最小值为$\frac{1}{2}$.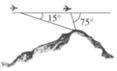 如图,飞机的航线和山顶在同一个铅垂平面内,已知飞机的高度为海拔15000 m,速度为1000 km/h,飞行员先看到山顶的俯角为15°,经过108s后又看到山顶的俯角为75°,则山顶的海拔高度为15-10$\sqrt{3}$km.
如图,飞机的航线和山顶在同一个铅垂平面内,已知飞机的高度为海拔15000 m,速度为1000 km/h,飞行员先看到山顶的俯角为15°,经过108s后又看到山顶的俯角为75°,则山顶的海拔高度为15-10$\sqrt{3}$km.