题目内容
设椭圆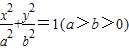 的左焦点为F,离心率为
的左焦点为F,离心率为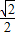 ,过点F且与x轴垂直的直线被椭圆截得的线段长为
,过点F且与x轴垂直的直线被椭圆截得的线段长为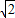 .
.(1)求椭圆方程.
(2)过点P(0,2)的直线l与椭圆交于不同的两点A,B,当△OAB面积最大时,求|AB|.
【答案】分析:(1)由椭圆的离心率和通径长及a2-b2=c2联立求出a,b的值,则椭圆方程可求;
(2)由题意设出直线方程,和椭圆方程联立后利用弦长公式求出弦长,由点到直线距离公式求出原点O到直线l的距离,利用换元法借助于不等式求出面积取最大值时的直线的斜率,从而求出直线被椭圆所截得的弦长.
解答:解:(1)由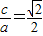 ,
,
又过点F且与x轴垂直的直线被椭圆截得的线段长为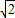 ,
,
得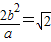 ,且a2-b2=c2,解得a2=2,b2=1.
,且a2-b2=c2,解得a2=2,b2=1.
所以椭圆方程为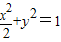 ;
;
(2)根据题意可知,直线l的斜率存在,故设直线l的方程为y=kx+2,
设A(x1,y1),B(x2,y2)
由方程组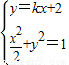 ,消去y得关于x的方程(1+2k2)x2+8kx+6=0
,消去y得关于x的方程(1+2k2)x2+8kx+6=0
由直线l与椭圆相交于A,B两点,则有△>0,
即64k2-24(1+2k2)=16k2-24>0,得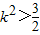
由根与系数的关系得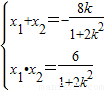
故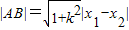
=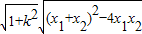 =
=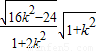
又因为原点O到直线l的距离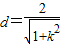 ,故△OAB的面积
,故△OAB的面积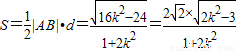
令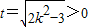 ,则2k2=t2+3
,则2k2=t2+3
所以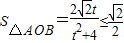 ,当且仅当t=2时等号成立,
,当且仅当t=2时等号成立,
即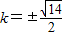 时,
时,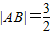 .
.
点评:本题考查了椭圆的标准方程,考查了直线和圆锥曲线的综合题,解答的关键是利用根与系数关系得到弦长,代入面积公式后借助于基本不等式求最值,考查了学生的计算能力,属有一定难度题目.
(2)由题意设出直线方程,和椭圆方程联立后利用弦长公式求出弦长,由点到直线距离公式求出原点O到直线l的距离,利用换元法借助于不等式求出面积取最大值时的直线的斜率,从而求出直线被椭圆所截得的弦长.
解答:解:(1)由
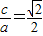 ,
,又过点F且与x轴垂直的直线被椭圆截得的线段长为
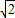 ,
,得
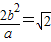 ,且a2-b2=c2,解得a2=2,b2=1.
,且a2-b2=c2,解得a2=2,b2=1.所以椭圆方程为
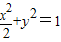 ;
;(2)根据题意可知,直线l的斜率存在,故设直线l的方程为y=kx+2,
设A(x1,y1),B(x2,y2)
由方程组
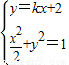 ,消去y得关于x的方程(1+2k2)x2+8kx+6=0
,消去y得关于x的方程(1+2k2)x2+8kx+6=0由直线l与椭圆相交于A,B两点,则有△>0,
即64k2-24(1+2k2)=16k2-24>0,得
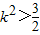
由根与系数的关系得
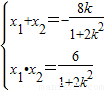
故
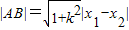
=
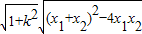 =
=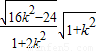
又因为原点O到直线l的距离
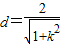 ,故△OAB的面积
,故△OAB的面积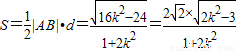
令
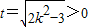 ,则2k2=t2+3
,则2k2=t2+3所以
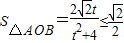 ,当且仅当t=2时等号成立,
,当且仅当t=2时等号成立,即
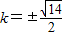 时,
时,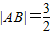 .
.点评:本题考查了椭圆的标准方程,考查了直线和圆锥曲线的综合题,解答的关键是利用根与系数关系得到弦长,代入面积公式后借助于基本不等式求最值,考查了学生的计算能力,属有一定难度题目.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
(本小题满分12分)
设椭圆![]() 的左焦点为F,O为坐标原点,已知椭圆中心关于直线
的左焦点为F,O为坐标原点,已知椭圆中心关于直线![]() 对称点恰好落在椭圆的左准线上。
对称点恰好落在椭圆的左准线上。
(1)求过O、F并且与椭圆右准线l相切的圆的方程;
|

 外的任意一点,过点P的直线PA、PB分别与椭圆相切于A、B两点。
外的任意一点,过点P的直线PA、PB分别与椭圆相切于A、B两点。 ,求直线
,求直线 的方程。
的方程。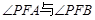 是否总是相等?若是,请给出证明。
是否总是相等?若是,请给出证明。 的左焦点为F, 离心率为
的左焦点为F, 离心率为 , 过点F且与x轴垂直的直线被椭圆截得的线段长为
, 过点F且与x轴垂直的直线被椭圆截得的线段长为 .
. 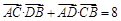 , 求k的值.
, 求k的值.