题目内容
在 中,角
中,角 所对的边分别是
所对的边分别是 ,已知
,已知 .
.
(1)若 的面积等于
的面积等于 ,求
,求 ;
;
(2)若 ,
, ,求
,求 的面积.
的面积.
(Ⅰ)2,2(Ⅱ)
解析试题分析:(Ⅰ)由 ,运用余弦定理可得
,运用余弦定理可得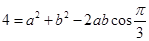 ,由
,由 的面积等于
的面积等于 ,运用三角形面积公式可得,
,运用三角形面积公式可得, ,联立即可解得
,联立即可解得 ;(Ⅱ)利用三角形内角和定理先将
;(Ⅱ)利用三角形内角和定理先将 化为
化为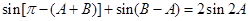 ,利用诱导公式及两角和与差的正弦公式将上式化为
,利用诱导公式及两角和与差的正弦公式将上式化为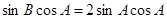 ,因为
,因为 ,若
,若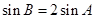 ,求出A,B关系,利用正弦定理求出
,求出A,B关系,利用正弦定理求出 关系,结合(Ⅰ)中结果
关系,结合(Ⅰ)中结果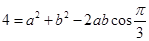 求出
求出 ,从而求出三角形面积.
,从而求出三角形面积.
试题解析:(Ⅰ)由余弦定理及已知条件得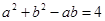
又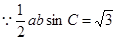 ,得
,得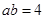 3分
3分
联立 解得
解得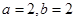 5分
5分
(Ⅱ)由题意得,
即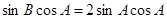 ,
, 又
又
 9分
9分 的面积
的面积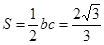 12分
12分
考点:正弦定理,余弦定理,三角形面积公式,三角变换,运算求解能力

练习册系列答案
相关题目
 sinA –cos(B+C)的取值范围.
sinA –cos(B+C)的取值范围. 。
。 的值;
的值; ,
,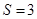 ,求
,求 的值.
的值.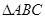 的内角
的内角 所对边的长分别是
所对边的长分别是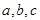 ,且
,且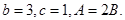
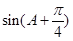 的值.
的值. 所对的边长分别为
所对的边长分别为 ,
, ,
, .
. 和
和 的值.
的值.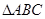 中,已知内角
中,已知内角 ,边
,边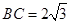 .设内角
.设内角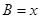 ,面积为
,面积为 .
.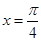 ,求边
,求边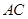 的长;
的长; ,
,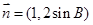 ,
,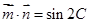 ,其中A,B,C分别为△ABC的三边
,其中A,B,C分别为△ABC的三边 ,
, ,
, 所对的角.
所对的角.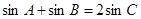 ,且S△ABC=
,且S△ABC= ,求边c的长
,求边c的长 中,
中, 是边
是边 上的点,且
上的点,且

 则
则 ____________
____________  中,已知
中,已知 ,
, ,
, ,则
,则 =
=