题目内容
对于无穷数列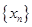 和函数
和函数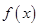 ,若
,若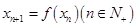 ,则称
,则称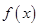 是数列
是数列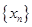 的母函数.
的母函数.
(Ⅰ)定义在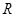 上的函数
上的函数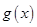 满足:对任意
满足:对任意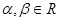 ,都有
,都有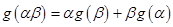 ,且
,且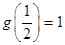 ;又数列
;又数列 满足:
满足: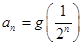 .
.
求证:(1)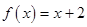 是数列
是数列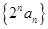 的母函数;
的母函数;
(2)求数列 的前项
的前项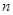 和
和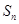 .
.
(Ⅱ)已知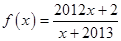 是数列
是数列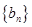 的母函数,且
的母函数,且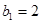 .若数列
.若数列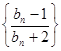 的前
的前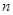 项和为
项和为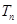 ,求证:
,求证: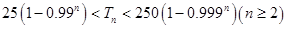 .
.
 和函数
和函数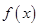 ,若
,若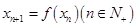 ,则称
,则称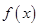 是数列
是数列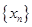 的母函数.
的母函数.(Ⅰ)定义在
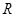 上的函数
上的函数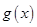 满足:对任意
满足:对任意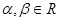 ,都有
,都有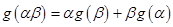 ,且
,且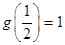 ;又数列
;又数列 满足:
满足: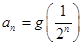 .
. 求证:(1)
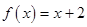 是数列
是数列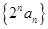 的母函数;
的母函数;(2)求数列
 的前项
的前项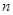 和
和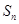 .
.(Ⅱ)已知
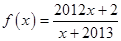 是数列
是数列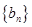 的母函数,且
的母函数,且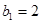 .若数列
.若数列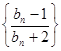 的前
的前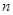 项和为
项和为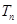 ,求证:
,求证: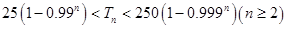 .
.(Ⅰ)(1) 由题知 ,
,

 ,
,
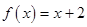 是数列
是数列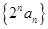 的母函数
的母函数
(2) (Ⅱ)
(Ⅱ) ,
,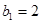 ,
,
 从而
从而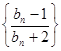 是以
是以 为首项,
为首项, 为公比的等比数列
为公比的等比数列
又 故当
故当 时,有
时,有

 ,化简得结论
,化简得结论
 ,
,

 ,
,
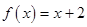 是数列
是数列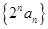 的母函数
的母函数(2)
 (Ⅱ)
(Ⅱ) ,
,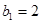 ,
,
 从而
从而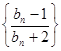 是以
是以 为首项,
为首项, 为公比的等比数列
为公比的等比数列
又
 故当
故当 时,有
时,有
 ,化简得结论
,化简得结论试题分析:(Ⅰ)(1)由题知
 ,且
,且

 .
.
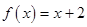 是数列
是数列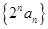 的母函数;
的母函数;(2) 由(1) 知:
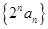 是首项和公差均为
是首项和公差均为 的等差数列,故
的等差数列,故 .
. ①
① ②
②①-②得:

 .
. .
.(Ⅱ)由题知:
 ,
,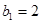 .
. 
 .
.从而
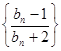 是以
是以 为首项,
为首项, 为公比的等比数列.
为公比的等比数列. .
.又

故当
 时,有:
时,有:


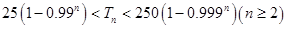 .
.点评:求解本题首先要正确理解所给信息母函数的实质,将其性质代入相应的函数式中推理;第一问的数列求和用到了错位相减法,这种方法是数列求和题常用到的方法,其适用于通项公式为关于n的一次函数式与指数式的乘积形式的数列

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的通项公式为
的通项公式为 ,其前
,其前 项和
项和 ,则双曲线
,则双曲线 的渐近线方程为( )
的渐近线方程为( )



 :
:
 ,设
,设 ,求
,求 。
。 ,
, 为数列
为数列 的前
的前 项和,求
项和,求 满足
满足 ,若
,若 ,则
,则 为
为



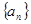 中, a2=7,且an =an+1-6(n∈
中, a2=7,且an =an+1-6(n∈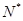 ),则前n项和Sn=" (" )
),则前n项和Sn=" (" )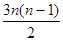
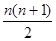
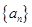 满足
满足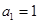 ,
,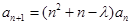 (
(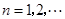 ),
),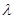 是常数.
是常数.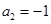 时,求
时,求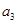 的值;
的值;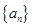 的前
的前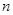 项和为
项和为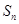 ,
,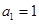 ,
,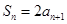 ,求
,求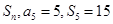 ,求数列
,求数列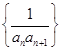 的前2012项和
的前2012项和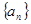 的前
的前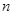 项和为
项和为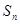 ,若
,若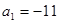 ,
,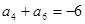 ,则当
,则当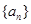 中,
中,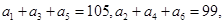 以
以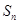 表示数列
表示数列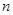 项和,则使
项和,则使


