题目内容
在直角△ABC中，两条直角边分别为a，b斜边和斜边上的高分别为c，h，则
的最大值为 ．
| c+h | a+b |
分析：如图所示，设A=θ，h=bsinθ，a=btanθ，c=
．可得
=
=
，令sinθ+cosθ=t，则t=
sin(θ+
)，可得1＜t≤
，1+2sinθcosθ=t2，于是sinθcosθ=
．可得
=
=
．令f（t）=
，利用导数即可得出．
| b |
| cosθ |
| c+h |
| a+b |
| ||
| btanθ+b |
| 1+sinθcosθ |
| sinθ+cosθ |
| 2 |
| π |
| 4 |
| 2 |
| t2-1 |
| 2 |
| c+h |
| a+b |
1+
| ||
| t |
| t2+1 |
| 2t |
| t2+1 |
| 2t |
解答：解：如图所示，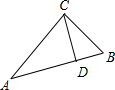
设A=θ，h=bsinθ，a=btanθ，c=
．
∴
=
=
，
令sinθ+cosθ=t，则t=
sin(θ+
)，
∵θ∈(0，
)，∴(θ+
)∈(
，
)，∴
＜sin(θ+
)≤1，
∴1＜t≤
．
由sinθ+cosθ=t，可得1+2sinθcosθ=t2，
∴sinθcosθ=
．
∴
=
=
．
令f（t）=
，
则f′（t）=
＞0．
∴f（t）在t∈(1，
]单调递增，
∴当t=
时，f（t）取得最大值，f(
)=
=
．
故答案为：
．
设A=θ，h=bsinθ，a=btanθ，c=
| b |
| cosθ |
∴
| c+h |
| a+b |
| ||
| btanθ+b |
| 1+sinθcosθ |
| sinθ+cosθ |
令sinθ+cosθ=t，则t=
| 2 |
| π |
| 4 |
∵θ∈(0，
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
| ||
| 2 |
| π |
| 4 |
∴1＜t≤
| 2 |
由sinθ+cosθ=t，可得1+2sinθcosθ=t2，
∴sinθcosθ=
| t2-1 |
| 2 |
∴
| c+h |
| a+b |
1+
| ||
| t |
| t2+1 |
| 2t |
令f（t）=
| t2+1 |
| 2t |
则f′（t）=
| t2-1 |
| 2t |
∴f（t）在t∈(1，
| 2 |
∴当t=
| 2 |
| 2 |
| 2+1 | ||
2
|
3
| ||
| 4 |
故答案为：
3
| ||
| 4 |
点评：本题考查了直角三角形的边角关系、三角函数的平方关系、三角函数的单调性、利用导数研究函数的单调性、换元法等基础知识与基本技能方法，考查了推理能力和计算能力，属于难题．
练习册系列答案
相关题目
在直角△ABC中，两直角边的长分别为a，b，直角顶点C到斜边的距离为h，则易证