题目内容
在直角△ABC中，两直角边的长分别为a，b，直角顶点C到斜边的距离为h，则易证| 1 |
| h2 |
| 1 |
| a2 |
| 1 |
| b2 |
分析：本题考查的知识点是类比推理，在由平面图形的性质向空间物体的性质进行类比时，常用的思路有：由平面图形中点的性质类比推理出空间里的线的性质，由平面图形中线的性质类比推理出空间中面的性质，由平面图形中面的性质类比推理出空间中体的性质．
解答：
解：类比得到：
=
+
+
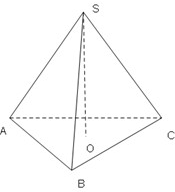
过S作△ABC所在平面的垂线，垂足为O，
连接CO并延长交AB于D，连接SD，
∵SO⊥平面ABC，
∴SO⊥AB
∵SC⊥SA，SC⊥SB，
∴SC⊥平面SAB，
∴SC⊥AB，SC⊥SD，
∴AB⊥平面SCD，
∴AB⊥SD
在Rt△ABS中，有
=
+
在Rt△CDS中，有
=
+
=
+
+
．
解：类比得到：| 1 |
| h2 |
| 1 |
| a2 |
| 1 |
| b2 |
| 1 |
| c2 |
过S作△ABC所在平面的垂线，垂足为O，
连接CO并延长交AB于D，连接SD，
∵SO⊥平面ABC，
∴SO⊥AB
∵SC⊥SA，SC⊥SB，
∴SC⊥平面SAB，
∴SC⊥AB，SC⊥SD，
∴AB⊥平面SCD，
∴AB⊥SD
在Rt△ABS中，有
| 1 |
| SD2 |
| 1 |
| a2 |
| 1 |
| b2 |
在Rt△CDS中，有
| 1 |
| h2 |
| 1 |
| SD2 |
| 1 |
| c2 |
| 1 |
| a2 |
| 1 |
| b2 |
| 1 |
| c2 |
点评：类比推理的一般步骤是：（1）找出两类事物之间的相似性或一致性；（2）用一类事物的性质去推测另一类事物的性质，得出一个明确的命题（猜想）．（3）对猜想的结论进行论证．
练习册系列答案
相关题目