题目内容
已知函数f(x)=ax2+bx+c(a≠0)满足f(0)=0,对于任意x∈R都有f( x)≥x,且f
x)≥x,且f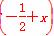 =f
=f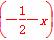 ,求函数f(x)的表达式.
,求函数f(x)的表达式.
解析:因为f(0)=0,所以c=0.
因为对于任意x∈R都有f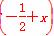 =f
=f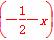 ,
,
所以函数f(x)的对称轴为x=-
 ,
,
即- =-
=- ,得a=b.
,得a=b.
对于任意x∈R都有f(x)≥x,
即ax2+(b-1)x≥0对于任意x∈R都成立,
所以a>0,且Δ=(b-1)2≤0.
因为(b-1)2≥0,  所以b=1,从而a=1.
所以b=1,从而a=1.
所以f(x)=x2+x.

练习册系列答案
相关题目
从一批苹果中,随机抽取50个,其重量(单位:克)的频数分布表如下:
| 分组(重量) | [80,85) | [85,90) | [90,95) | [95,100) |
| 频数(个) | 5 | 10 | 20 | 15 |
(1)根据频数分布表计算苹果的重量在[90,95)的频率;
(2)用分层抽样的方法从重量在[80,85)和[95,100)的苹果中共抽取4个,其中重量在[80,85)的有几个?
(3)在(2)中抽出的4个苹果中,任取2个,求重量在[80,85)和[ 95,100)中各有1个的概率.
95,100)中各有1个的概率.
 cos x+sin x,则f
cos x+sin x,则f (k为常数),如果不搞促销活动,则该产品的年销售量只能是1万件.已知2012年生产该产品的固
(k为常数),如果不搞促销活动,则该产品的年销售量只能是1万件.已知2012年生产该产品的固 定投入为8万元,每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).
定投入为8万元,每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).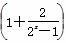 ·f(x)(x≠0)是偶函数,且f(x)不恒等于零,则 f(x)( )
·f(x)(x≠0)是偶函数,且f(x)不恒等于零,则 f(x)( ) )时x的取值范围.
)时x的取值范围.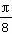 的概率是( )
的概率是( ) 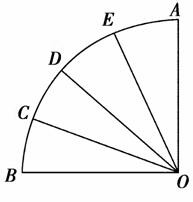
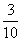 B.
B. C.
C.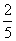 D.
D.