题目内容
已知函数f(x)=a·2x+b·3x,其中常数a,b满足ab≠0.
(1)若ab>0,判断函数f(x)的单调性;
(2)若ab<0,求f(x+1)>f(x )时x的取值范围.
)时x的取值范围.
解析:(1)当a>0,b>0时,任意x1,x2∈R ,x1<x2,则
,x1<x2,则
f (x1)-f(x2)=a(2x1-2x2)+b(3x1-3x2).
(x1)-f(x2)=a(2x1-2x2)+b(3x1-3x2).
∵2x1<2x2,a>0⇒a(2x1-2x2)<0,
3x1<3x2,b>0⇒b(3x1-3x2)<0,
∴f(x1)-f(x2)<0,函数f(x)在R上是增函数.
当a<0,b<0时,同理,函数f(x)在R上是减函数.
(2)f(x+1)-f(x)=a·2x+2b·3x>0.
当a<0,b>0时,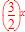 >-
>-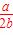 ,则x>log1.5
,则x>log1.5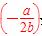 ;
;
当a>0,b<0时,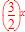 <-
<-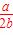 ,则x<log1.5
,则x<log1.5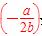

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目

 x)≥x,且f
x)≥x,且f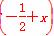 =f
=f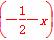 ,求函数f(x)的表达式.
,求函数f(x)的表达式. 满足f(a)=3,则f(a-5)的值
满足f(a)=3,则f(a-5)的值 为( )
为( ) C.
C. D.
D.

 量为185的样本,已知在高
量为185的样本,已知在高