题目内容
已知椭圆 经过点
经过点 ,且离心率为
,且离心率为
(1)求椭圆 的方程;
的方程;
 (2)设直线
(2)设直线 与椭圆
与椭圆 相较于
相较于 两点,
两点,
以线段 为邻边作平行四边形
为邻边作平行四边形 ,顶点
,顶点 恰好在椭
恰好在椭
圆 上,
上, 为坐标原点,求
为坐标原点,求 的取值范围。
的取值范围。
解:(Ⅰ)由已知: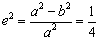 ,…①
,…①
又点 在椭圆上,所以
在椭圆上,所以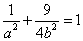 ,…②
,…②
联立①②解方程组,得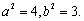
故椭圆 的方程为
的方程为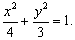 …………………………………………………5分
…………………………………………………5分
(Ⅱ)由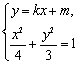 消去
消去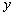 ,化简整理得
,化简整理得 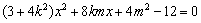 ,
,
因为直线l与椭圆 相交于
相交于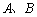 两点,
两点,
所以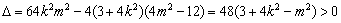 ,……③ ……7分
,……③ ……7分
设点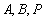 的坐标分别为
的坐标分别为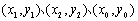 ,
,
因为OAPB是平行四边形,所以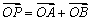 ,
,
即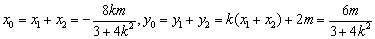 .……………9分
.……………9分
由于点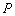 在椭圆
在椭圆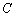 上,所以
上,所以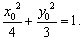
从而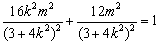 ,化简得
,化简得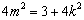 ,经检验符合题意又
,经检验符合题意又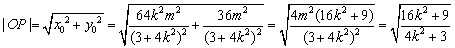
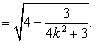
因为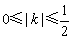 ,得
,得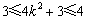 ,有
,有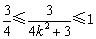 ,故
,故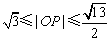 .
.
综上,所求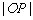 的取值范围是
的取值范围是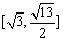

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目



 _________.
_________. -
- =-1的焦点为顶点,顶点为焦点的椭圆方程为( )
=-1的焦点为顶点,顶点为焦点的椭圆方程为( ) +
+ +
+ =1
=1 =1 D.
=1 D. 的实轴和虚轴的长、顶点和焦点的坐标、离心率.
的实轴和虚轴的长、顶点和焦点的坐标、离心率. 的定义域是( )
的定义域是( ) 的递减区间为______
的递减区间为______ ,
, ,
, ,
, ,则
,则 .
. 的左焦点为
的左焦点为 与过原点的直线相交于
与过原点的直线相交于 两点,连接
两点,连接 若
若 则
则 的离心率为
的离心率为  B.
B. C.
C. D.
D.