题目内容
各项均为正数的数列 中,
中,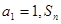 是数列
是数列 的前
的前 项和,对任意
项和,对任意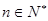 ,有
,有 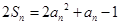 .
.
(1)求数列 的通项公式;
的通项公式;
(2)记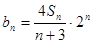 ,求数列
,求数列 的前
的前 项和
项和 .
.
(1)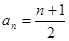 (2)
(2) 
解析试题分析:(1)根据题意利用 ,得到递推公式,根据其形式特点分析该数列的特点.
,得到递推公式,根据其形式特点分析该数列的特点.
(2)根据(1)求出 ,代入求出
,代入求出 ,根据其特点采用错位相减法求和.
,根据其特点采用错位相减法求和.
(1)由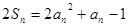 ①
①
得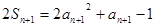 ②
②
②—①,得 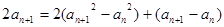
即: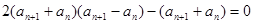
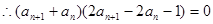
由于数列 各项均为正数,
各项均为正数, 即
即 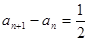
 数列
数列 是首项为
是首项为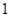 ,公差为
,公差为 的等差数列,
的等差数列, 数列
数列 的通项公式是
的通项公式是 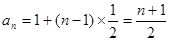
(2)由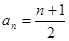 ,可得
,可得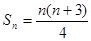 ,所以
,所以 ,根据特点采用错位相减法:
,根据特点采用错位相减法:
则

①-②得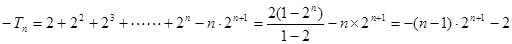

考点:已知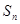 求
求 ;错位相减法求和.
;错位相减法求和.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
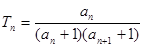 ,求证:
,求证: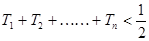 .
.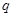 和
和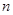 均为给定的大于1的自然数,设集合
均为给定的大于1的自然数,设集合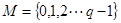 ,集合
,集合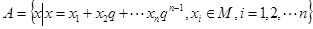 ,
,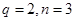 时,用列举法表示集合A;
时,用列举法表示集合A;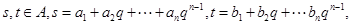 其中
其中 证明:若
证明:若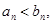 则
则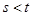 .
.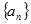 是公差不为零的等差数列,
是公差不为零的等差数列,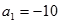 ,且
,且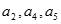 成等比数列.
成等比数列.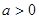 ,求数列
,求数列 的前n项和
的前n项和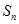 .
.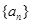 ,把
,把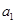 作为新数列
作为新数列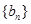 的第一项,把
的第一项,把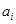 或
或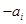 (
(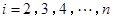 )作为新数列
)作为新数列 项,数列
项,数列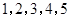 的一个生成数列是
的一个生成数列是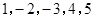 .已知数列
.已知数列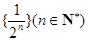 的生成数列,
的生成数列,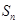 为数列
为数列 项和.
项和.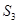 的所有可能值;
的所有可能值; ,求
,求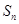 .
.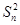 -(n2+n-1)Sn-(n2+n)=0.
-(n2+n-1)Sn-(n2+n)=0.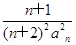 ,数列{bn}的前n项和为Tn,证明:对于任意的n∈N*,都有Tn<
,数列{bn}的前n项和为Tn,证明:对于任意的n∈N*,都有Tn< 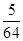 .
.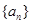 的首项
的首项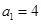 ,公差
,公差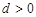 ,且
,且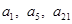 分别是正数等比数列
分别是正数等比数列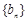 的
的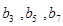 项.
项.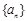 与
与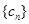 对任意
对任意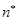 均有
均有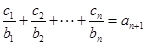 成立,设
成立,设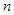 项和为
项和为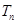 ,求
,求 的各项均为正数,其前
的各项均为正数,其前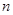 项和为
项和为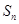 ,且
,且 .
.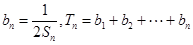 ,求证:
,求证: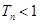 ;
;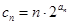 ,
,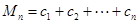 ,求
,求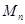 .
.