题目内容
已知数列{an}的前n项和为Sn,又a1=1,a2=2,且满足Sn+1=kSn+1,
(1)求k的值及{an}的通项公式;(2)若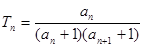 ,求证:
,求证: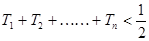 .
.
(1) ,(2)见解析
,(2)见解析
解析试题分析:(1)对于 ,取
,取 ,得
,得 ,结合
,结合 ,
, 即可求得
即可求得 ,对于求
,对于求 的通项,由
的通项,由 及
及 两式相减,可得
两式相减,可得 与
与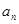 的关系,从而可知
的关系,从而可知 为特殊数列,进而求得其通项公式;(2)由
为特殊数列,进而求得其通项公式;(2)由 裂成
裂成 利用裂项相消法求得
利用裂项相消法求得 的前n项和,从而易得结论.
的前n项和,从而易得结论.
试题解析:(1)令 ,则
,则 ,因此
,因此 ,所以
,所以 ,
,
从而 ①,又
①,又 ②, 由①-②得,
②, 由①-②得, ,故
,故 , 又
, 又 ,所以
,所以 ;(2)因为
;(2)因为 ,故
,故
 ,得证.
,得证.
考点: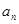 与
与 的关系:
的关系: ,数列求和方法:裂项相消法,特殊到一般的思想.
,数列求和方法:裂项相消法,特殊到一般的思想.

练习册系列答案
相关题目
 ,设曲线
,设曲线 在
在 处的切线与
处的切线与 轴交点的纵坐标为
轴交点的纵坐标为 ,则数列
,则数列 的前
的前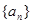 的各项均为正数,
的各项均为正数,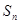 是数列
是数列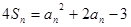 .
.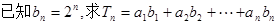 的值.
的值.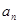 }是等差数列,数列{
}是等差数列,数列{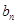 }的前
}的前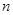 项和
项和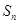 满足
满足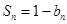 ,
,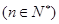 ,且
,且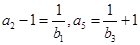
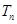 为数列{
为数列{ 中,
中,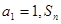 是数列
是数列 项和,对任意
项和,对任意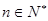 ,有
,有 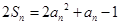 .
.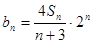 ,求数列
,求数列 的前
的前 .
.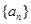 的通项
的通项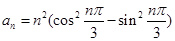 ,其前n项和为
,其前n项和为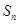 .
.  ;
;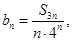 求数列{
求数列{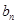 }的前n项和
}的前n项和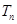 .
. 满足
满足 ,则
,则 =
= 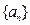 的前
的前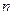 项和为
项和为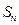 ,若
,若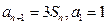 ,则通项
,则通项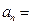 .
.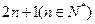 个正整数总和为
个正整数总和为 ,且这些数中后
,且这些数中后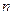 个数的平方和与前
个数的平方和与前 .若
.若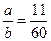 ,则
,则