题目内容
数列 的前几项和为
的前几项和为 ,满足
,满足 ,其中
,其中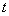 ﹥0
﹥0 。
。
⑴若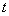 为常数,证明:数列
为常数,证明:数列 为等比数列;
为等比数列;
⑵若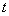 为变量,记数列
为变量,记数列 的公比为
的公比为 ,数列
,数列 满足
满足 ,求
,求 ,试判定
,试判定 与
与 的大小,并加以证明。
的大小,并加以证明。
解:(1)当 时,
时,
当 时,
时, ①
①
 ②
②
②-①得:

 ---------4分
---------4分
又 
故 是等比数列---------------6分
是等比数列---------------6分
(2)

猜想: ﹥
﹥ ------------8分
------------8分
下面用数学的归纳法证明:
当 ,则
,则 ﹥
﹥ 成立
成立
假设当 时,
时, ﹥
﹥
当 时,
时,


 ﹥
﹥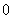
 即
即  ,结论也成立
,结论也成立
由①②知:  ﹥
﹥ ----------12分
----------12分

练习册系列答案
相关题目
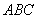 中,
中, 是
是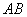 的中点,
的中点, 为线
为线 段
段 上一动点,则
上一动点,则 的取值范围为
的取值范围为 
 的图像向右平移
的图像向右平移 单位得到函数
单位得到函数 的图像,则将函
的图像,则将函 的图像,则
的图像,则 ( )
( ) B.
B. C.
C. D.
D.
 是等差数列,
是等差数列, 为其前
为其前 项和,若
项和,若 成等比数列,则
成等比数列,则 。
。
 ;
; ,若不等式
,若不等式 ﹥
﹥ 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。 )的图象大致是 ( )
)的图象大致是 ( )

 的最小值.
的最小值. 中,
中, ,
, ,
, ,点
,点 是
是 的中点
的中点 与
与 所成角的余弦值
所成角的余弦值 与
与 所成二面角的正弦值.
所成二面角的正弦值.