题目内容
8．给出下列一段推理：若一条直线平行于平面，则这条直线平行于平面内所有直线．已知直线a?平面α，直线b?平面α，且a∥α，所以a∥b．上述推理的结论不一定是正确的，其原因是（ ）| A． | 大前提错误 | B． | 小前提错误 | C． | 推理形式错误 | D． | 非以上错误 |
分析 分析该演绎推理的三段论，即可得出错误的原因是什么．
解答 解：该演绎推理的大前提是：若直线平行于平面，则该直线平行于平面内所有直线；
小前提是：已知直线a?平面α，直线b?平面α，且a∥α；
结论是：a∥b；
该结论是错误的，因为大前提是错误的，
正确叙述是“若直线平行于平面，过该直线作平面与已知平面相交，则交线与该直线平行”．
故选：A．
点评 本题通过演绎推理的三段论叙述，考查了空间中线面垂直的性质定理的应用问题，是基础题．
练习册系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
18．-150°的弧度数是（ ）
| A． | -$\frac{5π}{6}$ | B． | $\frac{4π}{3}$ | C． | -$\frac{2π}{3}$ | D． | -$\frac{3π}{4}$ |
13．2017年4月14日，某财经频道报道了某地建筑市场存在违规使用未经淡化海砂的现象．为了研究使用淡化海砂与混凝土耐久性是否达标有关，某大学实验室随机抽取了60个样本，得到了相关数据如表：
（Ⅰ）根据表中数据，求出s，t的值；
（Ⅱ）利用独立性检验的方法判断，能否在犯错误的概率不超过1%的前提下认为使用淡化海砂与混凝土耐久性是否达标有关？
参考数据：
参考公式：${K^2}=\frac{{n{{（{ad-bc}）}^2}}}{{（{a+b}）（{c+d}）（{a+c}）（{b+d}）}}$，其中n=a+b+c+d．
| 混凝土耐久性达标 | 混凝土耐久性不达标 | 总计 | |
| 使用淡化海砂 | 25 | t | 30 |
| 使用未经淡化海砂 | s | ||
| 总计 | 40 | 60 |
（Ⅱ）利用独立性检验的方法判断，能否在犯错误的概率不超过1%的前提下认为使用淡化海砂与混凝土耐久性是否达标有关？
参考数据：
| P（K2≥k0） | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
20．$\frac{i}{{\sqrt{7}+3i}}$=（ ）
| A． | $\frac{3}{16}-\frac{{\sqrt{7}}}{16}i$ | B． | $\frac{3}{16}+\frac{{\sqrt{7}}}{16}i$ | C． | $-\frac{3}{16}+\frac{{\sqrt{7}}}{16}i$ | D． | $-\frac{3}{16}-\frac{{\sqrt{7}}}{16}i$ |
17．已知命题p：?x∈R，x2+ax+a2≥0（a∈R），命题q：$?{x_0}∈{N^*}$，$2x_0^2-1≤0$，则下列命题中为真命题的是（ ）
| A． | p∧q | B． | p∨q | C． | （?p）∨q | D． | （?p）∧（?q） |
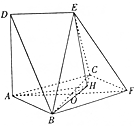如图，边长为2的正方形ABFC和高为2的直角梯形ADEF所在的平面互相垂直，AF∩BC=O，DE=$\sqrt{2}$，ED∥AF，且∠DAF=90°．