题目内容
试求满足方程![]() 的所有整数对
的所有整数对![]() .
.
满足原方程的全部整数对为:![]()
解析:
设整数对![]() 满足方程
满足方程![]() …(1),将其看作
…(1),将其看作
关于![]() 的一元二次方程,其判别式
的一元二次方程,其判别式![]() 的值
的值
应为一完全平方数;
若![]() ,则
,则![]() ;
;
若![]() ,则
,则![]() 可取
可取![]() ,相应的
,相应的![]() 值分别为
值分别为![]() 和
和![]() ,它们皆不为平方数;
,它们皆不为平方数;
因此,仅当![]() 时,
时,![]() 为完全平方数.
为完全平方数.
若![]() ,方程(1)化为
,方程(1)化为![]() , 解得
, 解得![]() 或
或![]() ;
;
若![]() ,方程(1)化为
,方程(1)化为 ![]() ,解得
,解得![]() 或
或![]() .
.
综上可知,满足原方程的全部整数对为:![]() .
.

练习册系列答案
相关题目

 的通项公式;
的通项公式; ,对任意
,对任意 在
在 之间插入
之间插入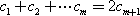 的所有正整数
的所有正整数 ,若存在正整数
,若存在正整数 成立,求
成立,求 的首项为
的首项为 ,公差为b,等比数列
,公差为b,等比数列 的首项为b,公比为a(其中a,b均为正整数)。
的首项为b,公比为a(其中a,b均为正整数)。 ,求数列
,求数列 的通项公式;
的通项公式; ,对任意
,对任意 在
在 之间插入
之间插入 个2,得到一个新的数列
个2,得到一个新的数列 ,试求满足等式
,试求满足等式 的所有正整数m的值;
的所有正整数m的值; ,若存在正整数m,n以及至少三个不同的b值使得等
,若存在正整数m,n以及至少三个不同的b值使得等 成立,求t的最小值,并求t最小时a,b的值。
成立,求t的最小值,并求t最小时a,b的值。