题目内容
已知F1、F2为双曲线
-
=1(a>0,b>0)的左、右焦点,P为该双曲线右支上一点,点P到右准线的距离为d,若|PF1|、|PF2|、d依次成等差数列,那么双曲线离心率的取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
A、(1,3-
| ||
B、(1,3-
| ||
C、(1,2+
| ||
D、(1,2+
|
考点:双曲线的简单性质
专题:综合题,圆锥曲线的定义、性质与方程
分析:根据双曲线的定义,结合等差数列的含义,得到|PF2|-|PF1|=d-|PF2|=-2a,再用圆锥曲线的统一定义,得到
=e,因此d-|PF2|=d(1-e)=-2a,得到d=
,最后根据双曲线右支上一点到右准线的距离的取值范围,得d≥a-
,建立关于a、c和e的不等式,解之即得此双曲线的离心率的取值范围.
| |PF2| |
| d |
| 2a |
| e-1 |
| a2 |
| c |
解答:
解:∵|PF1|、|PF2|、d依次成等差数列,
∴|PF2|-|PF1|=d-|PF2|,
∵P为双曲线
-
=1(a>0,b>0)右支上一点,(a>0,b>0)
∴|PF2|-|PF1|=-2a=d-|PF2|,
设双曲线的离心率是e,根据圆锥曲线的统一定义,
得到
=e,∴d-|PF2|=d(1-e)=-2a
∴根据双曲线右支上一点到右准线的距离的取值范围,得:d=
≥a-
,
上式的两边都除以a,得:
≥1-
,解此不等式得:2-
≤e≤2+
又∵双曲线的离心率e>1,
∴e∈(1,2+
].
故选:C
∴|PF2|-|PF1|=d-|PF2|,
∵P为双曲线
| x2 |
| a2 |
| y2 |
| b2 |
∴|PF2|-|PF1|=-2a=d-|PF2|,
设双曲线的离心率是e,根据圆锥曲线的统一定义,
得到
| |PF2| |
| d |
∴根据双曲线右支上一点到右准线的距离的取值范围,得:d=
| 2a |
| e-1 |
| a2 |
| c |
上式的两边都除以a,得:
| 2 |
| e-1 |
| 1 |
| e |
| 3 |
| 3 |
又∵双曲线的离心率e>1,
∴e∈(1,2+
| 3 |
故选:C
点评:本题以等差数列为载体,求双曲线的离心率,着重考查了双曲线的简单性质和等差数列的概念等知识点,属于中档题.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
命题“存在x1∈R,3 x1≤0”的否定是( )
| A、对任意的x∈R,3x>0 |
| B、对任意的x∈R,3x≤0 |
| C、不存在x1∈R,3 x1>0 |
| D、存在x1∈R,3 x1≥0 |
设
,
,
是任意的非零向量,且相互不共线,则
(1)(
•
)
-(
•
)
=0;
(2)若
•
=
•
,则
=
;
(3)|
|-|
|<|
-
|;
(4)(3
+2
)•(3
-2
)=9|
|2-4|
|2;
其中是真命题的有( )
| a |
| b |
| c |
(1)(
| a |
| b |
| c |
| c |
| a |
| b |
(2)若
| a |
| b |
| a |
| c |
| b |
| c |
(3)|
| a |
| b |
| a |
| b |
(4)(3
| a |
| b |
| a |
| b |
| a |
| b |
其中是真命题的有( )
| A、(1)(2) |
| B、(2)(3) |
| C、(3)(4) |
| D、(2)(4) |
已知各项均为正数的等比数列{an}中,lg(a3•a8•a13)=6,则a1•a15的值等于( )
| A、10000 | B、1000 |
| C、100 | D、10 |
已知
=(sinα,cosα),
=(sin
,cos
),且
⊥
,则符合要求的α为( )
| a |
| b |
| π |
| 4 |
| π |
| 4 |
| a |
| b |
A、
| ||
B、-
| ||
C、
| ||
D、
|
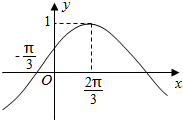 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(
| ||||
B、f(x)=2sin(
| ||||
C、f(x)=sin(
| ||||
D、f(x)=sin(
|
i是虚数单位,
=( )
| 3i |
| 2-i |
A、-
| ||||
B、-
| ||||
C、-
| ||||
D、-
|