题目内容
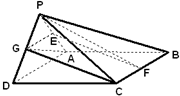 如图,△PAD为等边三角形,ABCD为矩形,平面PAD⊥平面ABCD,AB=2,E、F、G分别为PA、BC、PD中点,PC与底面ABCD成450角.
如图,△PAD为等边三角形,ABCD为矩形,平面PAD⊥平面ABCD,AB=2,E、F、G分别为PA、BC、PD中点,PC与底面ABCD成450角.(Ⅰ)求证:AG⊥EF
(Ⅱ)求二面角P-DF-A的正切.
分析:(Ⅰ)连接GE、GC,证明AG⊥平面PCD,可得AG⊥CG,再证明CG∥EF即可得到结论;
(Ⅱ)取AD中点H,连接PH,证明∠PCH是PC与平面ABCD所成的角,可求等边△PAD边长,过P做PK⊥DF于K,连接HK,则∠PKH就是二面角P-DF-A的平面角,利用正切函数可求二面角P-DF-A的正切值.
(Ⅱ)取AD中点H,连接PH,证明∠PCH是PC与平面ABCD所成的角,可求等边△PAD边长,过P做PK⊥DF于K,连接HK,则∠PKH就是二面角P-DF-A的平面角,利用正切函数可求二面角P-DF-A的正切值.
解答: (Ⅰ)证明:连接GE、GC
(Ⅰ)证明:连接GE、GC
∵△PAD是等边三角形,G为PD边中点,
∴AG⊥PD…(1分)
∵ABCD为矩形,∴CD⊥AD,
∵平面PAD⊥平面ABCD,
∴CD⊥平面PAD…(2分)
∴CD⊥AG,∴AG⊥平面PCD,∴AG⊥CG…(3分)
∵E、F分别为PA、BC中点,
∴GE
AD,CF
AD,∴GE
CF,
∴四边形CFEG是平行四边形,∴CG∥EF…(4分)
∴AG⊥EF…(5分)
(Ⅱ)解:(图1)取AD中点H,连接PH,在等边△PAD中,PH⊥AD,则PH⊥平面ABCD,∴PH⊥CH且∠PCH是PC与平面ABCD所成的角,∴∠PCH=45°,…(7分)
设等边△PAD边长为a,则PH=HC=
a,DH=
a
∵在矩形ABCD中,AB=2,
∴4=CD2=CH2-DH2=
a2-
a2=
a2
解得a=2
…(9分)
∵PH⊥平面ABCD,∴PH⊥DF
过P做PK⊥DF于K,连接HK,则DF⊥平面PHK,则∠PKH就是二面角P-DF-A的平面角…(11分)
由DF=
及s△ADF=
×2HK•DF=
AB•AD解得HK=
∴在Rt△PDF中,tan∠PKH=
=
…(12分)
∴求二面角P-DF-A的正切值为
…(14分)
 (Ⅰ)证明:连接GE、GC
(Ⅰ)证明:连接GE、GC∵△PAD是等边三角形,G为PD边中点,
∴AG⊥PD…(1分)
∵ABCD为矩形,∴CD⊥AD,
∵平面PAD⊥平面ABCD,
∴CD⊥平面PAD…(2分)
∴CD⊥AG,∴AG⊥平面PCD,∴AG⊥CG…(3分)
∵E、F分别为PA、BC中点,
∴GE
| ||
. |
| 1 |
| 2 |
| ||
. |
| 1 |
| 2 |
| ||
. |
∴四边形CFEG是平行四边形,∴CG∥EF…(4分)
∴AG⊥EF…(5分)
(Ⅱ)解:(图1)取AD中点H,连接PH,在等边△PAD中,PH⊥AD,则PH⊥平面ABCD,∴PH⊥CH且∠PCH是PC与平面ABCD所成的角,∴∠PCH=45°,…(7分)
设等边△PAD边长为a,则PH=HC=
| ||
| 2 |
| 1 |
| 2 |
∵在矩形ABCD中,AB=2,
∴4=CD2=CH2-DH2=
| 3 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
解得a=2
| 2 |
∵PH⊥平面ABCD,∴PH⊥DF
过P做PK⊥DF于K,连接HK,则DF⊥平面PHK,则∠PKH就是二面角P-DF-A的平面角…(11分)
由DF=
| 6 |
| 1 |
| 2 |
| 1 |
| 2 |
2
| ||
| 3 |
∴在Rt△PDF中,tan∠PKH=
| PH |
| HK |
3
| ||
| 2 |
∴求二面角P-DF-A的正切值为
3
| ||
| 2 |
点评:本题考查线线垂直,考查面面角,解题的关键是证明线面垂直,正确作出面面角,属于中档题.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
 (2012•烟台二模)如图,△PAD为等边三角形,ABCD为矩形,平面PAD⊥平面ABCD,AB=2,E、F、G分别为PA、BC、PD中点,
(2012•烟台二模)如图,△PAD为等边三角形,ABCD为矩形,平面PAD⊥平面ABCD,AB=2,E、F、G分别为PA、BC、PD中点, 如图,△PAD为等边三角形,ABCD为矩形,平面PAD⊥平面ABCD,AB=2,E、F、G分别为PA、BC、PD中点,AD=2
如图,△PAD为等边三角形,ABCD为矩形,平面PAD⊥平面ABCD,AB=2,E、F、G分别为PA、BC、PD中点,AD=2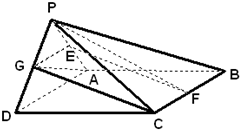 如图,△PAD为等边三角形,ABCD为矩形,平面PAD平面ABCD,AB=2,E、F、G分别为PA、BC、PD中点,AD=
如图,△PAD为等边三角形,ABCD为矩形,平面PAD平面ABCD,AB=2,E、F、G分别为PA、BC、PD中点,AD=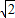 .
.