题目内容
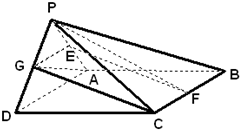 如图,△PAD为等边三角形,ABCD为矩形,平面PAD平面ABCD,AB=2,E、F、G分别为PA、BC、PD中点,AD=2
如图,△PAD为等边三角形,ABCD为矩形,平面PAD平面ABCD,AB=2,E、F、G分别为PA、BC、PD中点,AD=2| 2 |
(Ⅰ)求证:AB⊥平面PAD
(Ⅱ)求多面体P-AGF的体积.
分析:(Ⅰ)利用面面垂直的性质,证明线面垂直即可;
(II)判断点F到平面PAD的距离等于AB.由此可得三棱锥F-PAG的体积V,即为多面体P-AGF的体积.
(II)判断点F到平面PAD的距离等于AB.由此可得三棱锥F-PAG的体积V,即为多面体P-AGF的体积.
解答: (Ⅰ)证明:∵ABCD为矩形,∴AB⊥AD
(Ⅰ)证明:∵ABCD为矩形,∴AB⊥AD
又平面PAD⊥平面ABCD,且平面PAD∩平面ABCD=AD,AB?平面ABCD,
∴AB⊥平面PAD
(Ⅱ)解:由(I)得AB⊥平面PAD,
∵BC∥AD,AD?平面PAD,BC?平面PAD,∴BC∥平面PAD,
∴点F到平面PAD的距离等于AB
∴三棱锥F-PAG的体积为:V=
×AB×S△PAG=
×2×
×
×(2
)2=
.
 (Ⅰ)证明:∵ABCD为矩形,∴AB⊥AD
(Ⅰ)证明:∵ABCD为矩形,∴AB⊥AD又平面PAD⊥平面ABCD,且平面PAD∩平面ABCD=AD,AB?平面ABCD,
∴AB⊥平面PAD
(Ⅱ)解:由(I)得AB⊥平面PAD,
∵BC∥AD,AD?平面PAD,BC?平面PAD,∴BC∥平面PAD,
∴点F到平面PAD的距离等于AB
∴三棱锥F-PAG的体积为:V=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 4 |
| 2 |
2
| ||
| 3 |
点评:本题考查线面垂直、考查锥体的体积,正确运用面面垂直的性质是关键,属于中档题.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
 (2012•烟台二模)如图,△PAD为等边三角形,ABCD为矩形,平面PAD⊥平面ABCD,AB=2,E、F、G分别为PA、BC、PD中点,
(2012•烟台二模)如图,△PAD为等边三角形,ABCD为矩形,平面PAD⊥平面ABCD,AB=2,E、F、G分别为PA、BC、PD中点, 如图,△PAD为等边三角形,ABCD为矩形,平面PAD⊥平面ABCD,AB=2,E、F、G分别为PA、BC、PD中点,AD=2
如图,△PAD为等边三角形,ABCD为矩形,平面PAD⊥平面ABCD,AB=2,E、F、G分别为PA、BC、PD中点,AD=2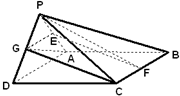 如图,△PAD为等边三角形,ABCD为矩形,平面PAD⊥平面ABCD,AB=2,E、F、G分别为PA、BC、PD中点,PC与底面ABCD成450角.
如图,△PAD为等边三角形,ABCD为矩形,平面PAD⊥平面ABCD,AB=2,E、F、G分别为PA、BC、PD中点,PC与底面ABCD成450角.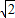 .
.