题目内容
如图,△PAD为等边三角形,ABCD为矩形,平面PAD⊥平面ABCD,AB=2,E、F、G分别为PA、BC、PD中点,AD=2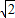 .
.(Ⅰ)求证:EF∥平面PCD.
(Ⅱ)求证:AG⊥EF
(Ⅲ)求多面体P-AGF的体积.

【答案】分析:(Ⅰ)由ABCD为矩形,知AD||BC,AD=BC,由E,F,G分别为PA,BC,PD中点,导出四形CFEG是平行四形,由此能够证明EF∥平面PCD.
(Ⅱ)由△PAD是等三角形,G为PD边的中点.知AG⊥PD,由此能够证明AG⊥EF.
(Ⅲ)由V三棱柱P-AFG=V三棱柱F-PAG,能够求出多面体P-AGF的体积.
解答:(Ⅰ)证明:∵ABCD为矩形,
∴AD||BC,AD=BC,
又∵E,F,G分别为PA,BC,PD中点,
∴GE∥AD,GE= ,∴CF∥AD,CF=
,∴CF∥AD,CF= ,
,
∴GE∥CF,GE=CF,∴四形CFEG是平行四形,
∴CG∥EF,
又∵EF?平面PCD,CG?平面PCD,∴EF∥平面PCD.
(Ⅱ)证明:∵△PAD是等三角形,G为PD边的中点.
∴AG⊥PD,∵平面PAD⊥平面ABCD,∴CD⊥平面PAD,
∴CD⊥AG,∴AG⊥平面PCD,
∵CG∥EF,∴AG⊥EF.
(Ⅲ)解:V三棱柱P-AFG=V三棱柱F-PAG,
=
= ×
× .
.
点评:本题考查直线与平面的平行的证明,考查直线与直线垂直的证明,考查多面体体积的求法.解题时要认真审题,仔细解答,注意等价转化思想的合理运用.
(Ⅱ)由△PAD是等三角形,G为PD边的中点.知AG⊥PD,由此能够证明AG⊥EF.
(Ⅲ)由V三棱柱P-AFG=V三棱柱F-PAG,能够求出多面体P-AGF的体积.
解答:(Ⅰ)证明:∵ABCD为矩形,
∴AD||BC,AD=BC,
又∵E,F,G分别为PA,BC,PD中点,
∴GE∥AD,GE=
 ,∴CF∥AD,CF=
,∴CF∥AD,CF= ,
,∴GE∥CF,GE=CF,∴四形CFEG是平行四形,
∴CG∥EF,
又∵EF?平面PCD,CG?平面PCD,∴EF∥平面PCD.
(Ⅱ)证明:∵△PAD是等三角形,G为PD边的中点.
∴AG⊥PD,∵平面PAD⊥平面ABCD,∴CD⊥平面PAD,
∴CD⊥AG,∴AG⊥平面PCD,
∵CG∥EF,∴AG⊥EF.
(Ⅲ)解:V三棱柱P-AFG=V三棱柱F-PAG,
=

=
 ×
× .
.点评:本题考查直线与平面的平行的证明,考查直线与直线垂直的证明,考查多面体体积的求法.解题时要认真审题,仔细解答,注意等价转化思想的合理运用.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
 (2012•烟台二模)如图,△PAD为等边三角形,ABCD为矩形,平面PAD⊥平面ABCD,AB=2,E、F、G分别为PA、BC、PD中点,
(2012•烟台二模)如图,△PAD为等边三角形,ABCD为矩形,平面PAD⊥平面ABCD,AB=2,E、F、G分别为PA、BC、PD中点, 如图,△PAD为等边三角形,ABCD为矩形,平面PAD⊥平面ABCD,AB=2,E、F、G分别为PA、BC、PD中点,AD=2
如图,△PAD为等边三角形,ABCD为矩形,平面PAD⊥平面ABCD,AB=2,E、F、G分别为PA、BC、PD中点,AD=2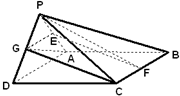 如图,△PAD为等边三角形,ABCD为矩形,平面PAD⊥平面ABCD,AB=2,E、F、G分别为PA、BC、PD中点,PC与底面ABCD成450角.
如图,△PAD为等边三角形,ABCD为矩形,平面PAD⊥平面ABCD,AB=2,E、F、G分别为PA、BC、PD中点,PC与底面ABCD成450角.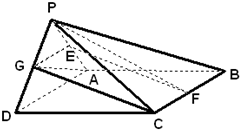 如图,△PAD为等边三角形,ABCD为矩形,平面PAD平面ABCD,AB=2,E、F、G分别为PA、BC、PD中点,AD=
如图,△PAD为等边三角形,ABCD为矩形,平面PAD平面ABCD,AB=2,E、F、G分别为PA、BC、PD中点,AD=