题目内容
已知函数 .
.
(Ⅰ)若曲线 在
在 和
和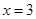 处的切线互相平行,求
处的切线互相平行,求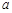 的值;
的值;
(Ⅱ)求 的单调区间;
的单调区间;
(Ⅲ)设 ,若对任意
,若对任意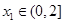 ,均存在
,均存在 ,使得
,使得 ,求
,求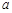 的取值范围.
的取值范围.
(Ⅰ)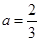 ;(2)单调递增区间是
;(2)单调递增区间是 和
和 ,单调递减区间是
,单调递减区间是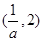 ;(3)
;(3)
解析试题分析:(Ⅰ)由函数 ,得
,得 ,又由曲线
,又由曲线 在
在 和
和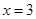 处的切线互相平行,则两切线的斜率相等地,即
处的切线互相平行,则两切线的斜率相等地,即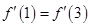 ,因此可以得到关于
,因此可以得到关于 的等式
的等式 ,从而可求出
,从而可求出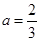 .
.
(Ⅱ)由 ,令
,令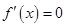 ,则
,则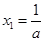 ,
, ,因此需要对
,因此需要对 与0,
与0, ,2比较进行分类讨论:①当
,2比较进行分类讨论:①当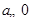 时,在区间
时,在区间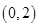 上有
上有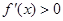 ,在区间
,在区间 上有
上有 ;②当时
;②当时 ,在区间
,在区间 和
和 上有
上有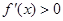 ,在区间
,在区间 上有
上有 ;③当时
;③当时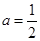 ,有
,有 ;④当
;④当 时,区间
时,区间 和
和 上有
上有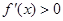 ,在区间
,在区间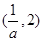 上有
上有 ,综上得
,综上得 的单调递增区间是
的单调递增区间是 和
和 ,单调递减区间是
,单调递减区间是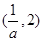 .
.
(Ⅲ)由题意可知,在区间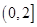 上有函数
上有函数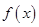 的最大值小于
的最大值小于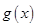 的最大值成立,又函数
的最大值成立,又函数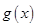 在
在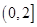 上的最大值
上的最大值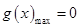 ,由(Ⅱ)知,①当
,由(Ⅱ)知,①当 时,
时, 在
在 上单调递增,故
上单调递增,故 ,所以,
,所以, ,解得
,解得 ,故
,故 ;②当
;②当 时,
时, 在
在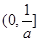 上单调递增,在
上单调递增,在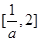 上单调递减,
上单调递减,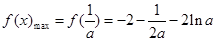 ,由
,由 可知
可知 ,
, ,
, ,所以,
,所以, ,
,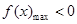 ;综上所述,所求
;综上所述,所求 的范围为
的范围为 .
.
试题解析:
 . 2分
. 2分
(Ⅰ) ,解得
,解得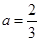 . 3分
. 3分
(Ⅱ)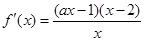
 . 5分
. 5分
①当 时,
时,

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
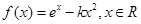 .
.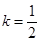 ,求证:当
,求证:当 时,
时, ;
; 在区间
在区间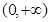 上单调递增,试求
上单调递增,试求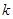 的取值范围;
的取值范围;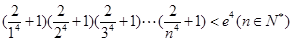 .
. 的正方形
的正方形 内建一个交通“环岛”.正方形的四个顶点为圆心在四个角分别建半径为
内建一个交通“环岛”.正方形的四个顶点为圆心在四个角分别建半径为 (
( 不小于
不小于 )的扇形花坛,以正方形的中心为圆心建一个半径为
)的扇形花坛,以正方形的中心为圆心建一个半径为 的圆形草地.为了保证道路畅通,岛口宽不小于
的圆形草地.为了保证道路畅通,岛口宽不小于 ,绕岛行驶的路宽均不小于
,绕岛行驶的路宽均不小于 .
.
 取
取 )
) 元
元 ,四个花坛的造价为
,四个花坛的造价为 元
元 元
元 ,
, .
. 与
与 在
在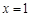 处相切,试求
处相切,试求 在
在 上是减函数,求实数
上是减函数,求实数 的取值范围;
的取值范围;
 .
. ,其中
,其中
 是自然对数的底数.
是自然对数的底数.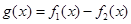 的零点;
的零点;
 均有两个极值点,一个在区间
均有两个极值点,一个在区间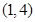 内,另一个在区间
内,另一个在区间 外,
外, 的取值范围;
的取值范围; 且函数
且函数 在
在 上是单调函数,探究函数
上是单调函数,探究函数 的单调性.
的单调性. 是二次函数,不等式
是二次函数,不等式 的解集是
的解集是 ,且
,且 处的切线与直线
处的切线与直线 平行.
平行. 在区间
在区间 内有两个不等的实数根?
内有两个不等的实数根? 在x=0,x=
在x=0,x= 处存在极值。
处存在极值。 .
. ,求曲线
,求曲线 在点
在点 处的切线方程;
处的切线方程; 的单调性.
的单调性. 为
为 的
的 阶函数.
阶函数. 的单调区间;
的单调区间; 的解的个数;
的解的个数; .
.