题目内容
20.已知函数f(x)=$\left\{\begin{array}{l}{(\frac{1}{2})^{x},x≤1}\\{-{x}^{2}+4x-\frac{5}{2},x>1}\end{array}\right.$,若函数g(x)=$\frac{3}{2}$x-a,其中a∈R,若函数y=f(x)-g(x)恰有3个零点,则实数a的取值范围是( )| A. | (0,$\frac{15}{16}$) | B. | ($\frac{15}{16}$,1) | C. | (1,$\frac{16}{15}$) | D. | (1,$\frac{5}{4}$) |
分析 由y=f(x)-g(x)=0得f(x)=g(x),作出两个函数f(x)和g(x)的图象,利用数形结合进行求解即可.
解答 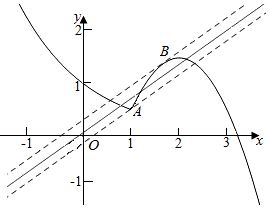 解:由y=f(x)-g(x)=0得f(x)=g(x),作出两个函数f(x)和g(x)的图象,
解:由y=f(x)-g(x)=0得f(x)=g(x),作出两个函数f(x)和g(x)的图象,
则A(1,$\frac{1}{2}$),
当g(x)经过点A时,f(x)与g(x)有2个交点,此时g(1)=$\frac{3}{2}$-a=$\frac{1}{2}$,此时a=1,
当g(x)与f(x)在x>1相切时,此时f(x)与g(x)有2个交点
由-x2+4x-$\frac{5}{2}$=$\frac{3}{2}$x-a,
即x2-$\frac{5}{2}$x+$\frac{5}{2}$-a=0,
由判别式△=0得($\frac{5}{2}$)2-4($\frac{5}{2}$-a)=0,
得a=$\frac{15}{16}$,
要使f(x)与g(x)有3个交点,则g(x)位于这两条线之间,
则a满足a∈($\frac{15}{16}$,1),
故选:B
点评 本题主要考查函数与方程的应用,利用条件转化为两个函数的交点问题,利用数形结合作出两个函数的图象是解决本题的关键.综合性较强.

练习册系列答案
相关题目
13.已知x>y>z>1,log2($\frac{x}{z}$)•[log${\;}_{(\frac{x}{y})}$2+log${\;}_{(\frac{y}{z})}$16]=9,则( )
| A. | y3=x2z | B. | y3=xz2 | C. | y2=xz | D. | 2y3=3xz2 |
12.复数$\frac{2-i}{1+i}$的共轭复数在复平面上对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
9.已知i是虚数单位,若1+i=z(1-i),则z=( )
| A. | -1 | B. | 1 | C. | -i | D. | i |
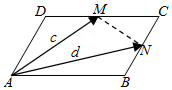 (1)如图,平行四边形ABCD中,M、N分别为DC、BC的中点,已知$\overrightarrow{AM}=\overrightarrow{c}$、$\overrightarrow{AN}=\overrightarrow{d}$,试用$\overrightarrow{c}$、$\overrightarrow{d}$表示$\overrightarrow{AB}$和$\overrightarrow{AD}$.
(1)如图,平行四边形ABCD中,M、N分别为DC、BC的中点,已知$\overrightarrow{AM}=\overrightarrow{c}$、$\overrightarrow{AN}=\overrightarrow{d}$,试用$\overrightarrow{c}$、$\overrightarrow{d}$表示$\overrightarrow{AB}$和$\overrightarrow{AD}$.